The forces that bind protons and neutrons in an atomic nucleus are so strong that when they break, there is a nuclear explosion. This power is needed to overcome the electric repulsion between protons, so the force holding the nucleus together was called the strong force. It has the odd property that it is zero at short range but increases with distance, like stretching a rubber band. It exchanges no energy so it isn’t electromagnetic, and increases with distance so it isn’t gravity. The standard model needed a new force to hold the nucleus together.
Its answer was quantum chromo-dynamics (QCD), a field theory based on quantum electro-dynamics (QED). QED explains electro-magnetism as perturbations in an electro-magnetic field that absorbs and emits photons, as in Feynman diagrams. Aiming to repeat this success, QCD proposed a new strong field that emitted gluon particles with color charges.
Simply put, strong field gluons act to cause effects like electro-magnetic field photons do, but with three charges (red, blue, and green) that cancel to white, instead of two charges that cancel to neutral. Three colors needed anti-colors to work, so to turn a red quark blue needs an anti-red gluon as well as a blue gluon. It was tricky but the calculations were made to work, so when in 1978 the PLUTO project managed to interpret a three-jet Upsilon event in gluon terms, gluons joined the standard model particle pantheon. No-one asked why a field that exists through all space was needed just for quarks.
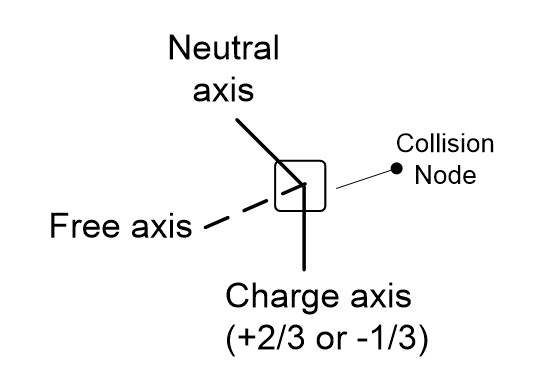
A processing model based on reverse engineering approaches the same facts differently. The quark structure in Figure 4.11 has free photons in one axis that could insert themselves into another quark nearby in a plasma. In Figure 4.12, an extreme photon head is in one quark and its tail in another, so side-by-side quarks could connect like this.
The resulting bond is initially zero but increases as the quarks separate, since the shared photon wavelength increases to release the energy that pulls them back together.
.
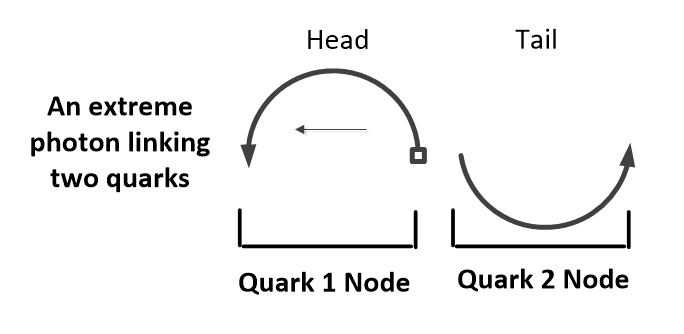
The further apart the quarks, the stronger the effect, so side-by-side quarks experience no force unless they move apart. Shared photons could then be the elastic bands that bind quarks in the nucleus, not gluons from a strong field, but how then do protons and neutrons form?