The standard model of physics took over a century to build and summarizes:
“… in a remarkably compact form, almost everything we know about the fundamental laws of physics.”(Wilczek, 2008) (p164)
It is currently considered by physicists to be:
“…truly the crowning scientific accomplishment of the twentieth century.” (Oerter, 2006) p75.
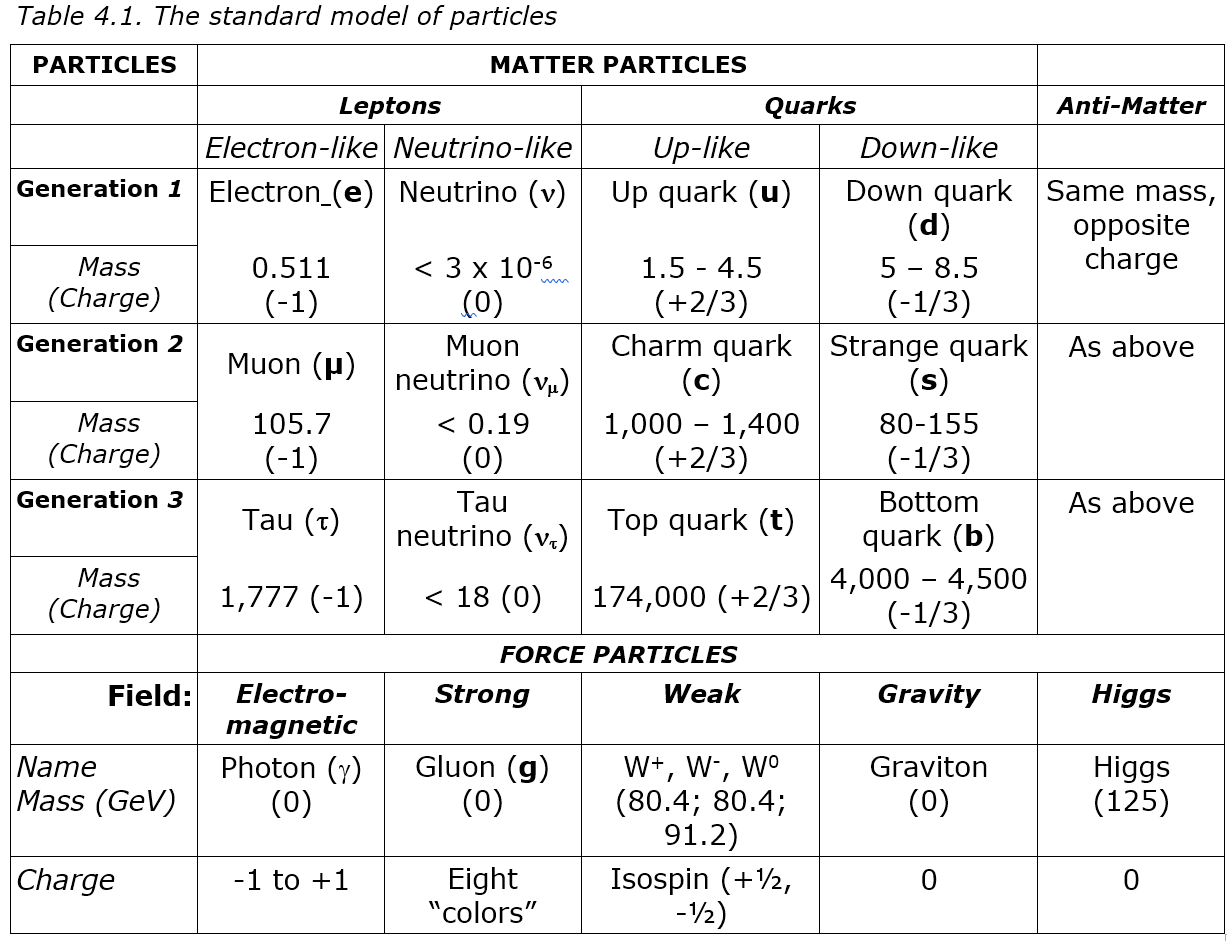
The standard model considers all reality to consist of particles, which it divides into matter particles called fermions and force particles called bosons (Table 4.1). Physics currently attributes all matter to fermion particles and all forces to boson particles, where fermions collide with each other and bosons don’t.
Matter particles divide into leptons like the electron and neutrino, and quarks that can be up or down. Both have unstable higher generations for some unknown reason. Up and down quarks combine into the protons and neutrons of atomic nuclei that with electrons form the atoms of ordinary matter. Apart from neutrinos that whizz around for no reason and anti-matter that was expected but is nowhere to be found, it all seems fairly tidy, but as Woit notes:
“By 1973, physicists had in place what was to become a fantastically successful theory … that was soon to acquire the name of the ‘standard model’. Since that time, the overwhelming triumph of the standard model has been matched by a similarly overwhelming failure to find any way to make further progress on fundamental questions.” (Woit, 2007) p1
Some fundamental questions the standard model doesn’t answer include:
- Why don’t protons decay as neutrons do?
- Why is our universe made of matter not anti-matter?
- Why do neutrinos have a tiny but variable mass?
- Why do leptons and quarks have three particle “generations” then no more?
- Why do electrons “half spin”?
- Why do particle masses vary enormously but charges don’t?
- Why do neutrinos always have left-handed spin?
- Why do quarks have one-third charges?
- Why does the force binding quarks increase as they move apart?
- What is the dark matter and dark energy that constitute most of the universe?
It isn’t just that these questions are unanswered but that over fifty years has seen no progress at all in answering them. The great hopes of string theory and super-symmetry led nowhere so the next fifty years look like being the same. Can a quantum processing model make progress where the standard model can’t?