Euclid extended a point three times to get three linear dimensions, so would three orthogonal rotations around a point give three polar dimensions? It would, but after the first two rotations give a circle and a sphere, our space has no more dimensions to rotate into. Yet in mathematics, rotating a sphere in an orthogonal direction gives a hypersphere. A hypersphere is a sphere rotated in another dimension as a sphere is a circle rotated in another dimension, so its surface has three dimensions (Figure 2.5).
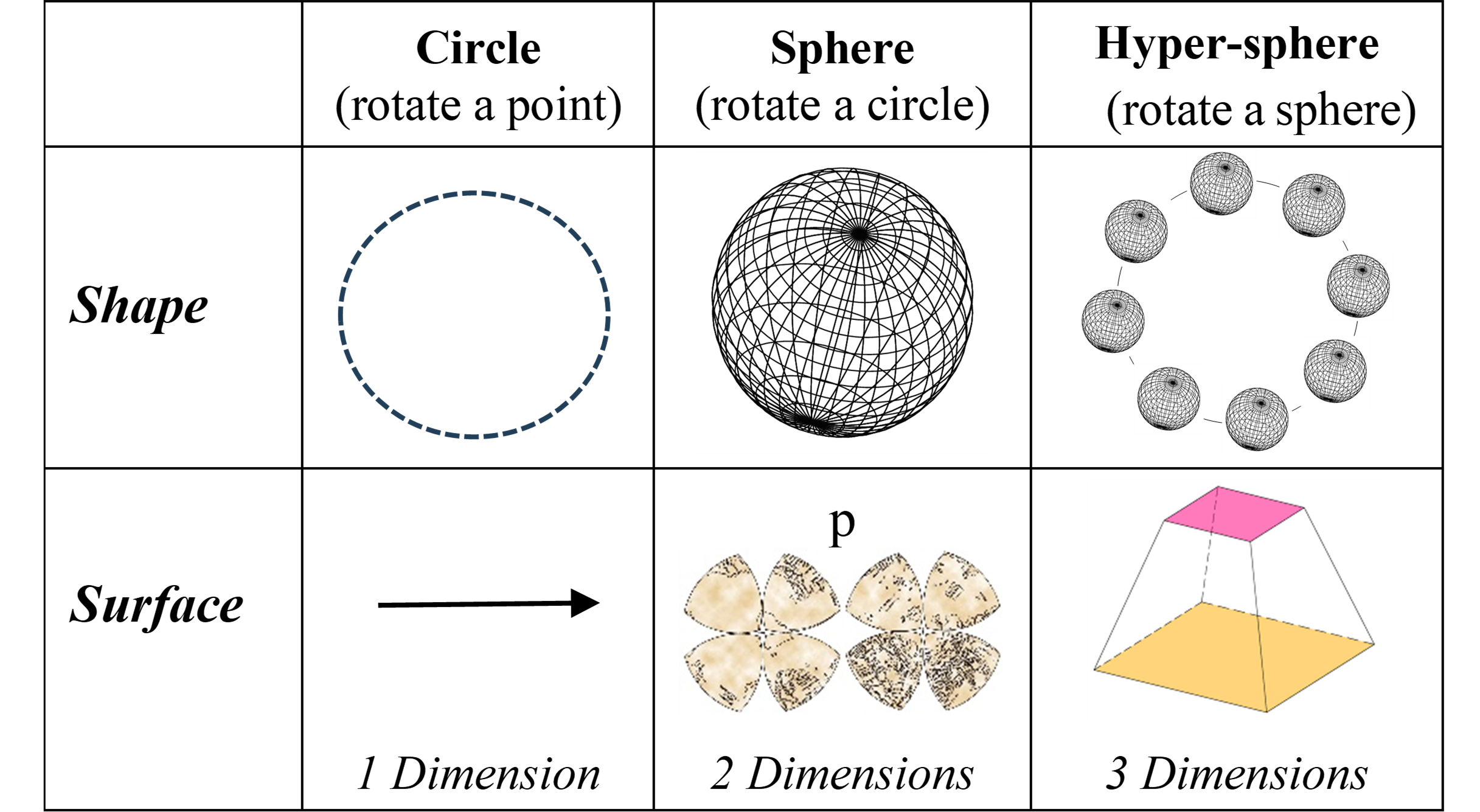
The possibility that our space is a surface was introduced by Bernard Riemann in 1857, as his Riemann Sphere is a hypersphere whose surface has three dimensions, just like our space. It still applies today because relativity lets space curve like a surface and cosmology lets it expand like a surface. It follows that our space could be a three-dimensional surface within a four-dimensional bulk:
“When it comes to the visible universe the situation could be subtle. The three-dimensional volume of space might be the surface area of a four dimensional volume” (Barrow, 2007) p180.
Davies makes the case even more clearly:
“… the shape of space resembles a three-dimensional version of the surface of a sphere, which is called a hypersphere.” (P. Davies, 2006), p45.
The mathematics is solid, but a hypersphere needs a fourth dimension outside physical space. Our space doesn’t have four degrees of freedom but the network generating it could have. Just as a three-dimensional network can represent a circle and a sphere, so a four-dimensional network can represent a hypersphere. Our space would then be a three-dimensional surface, just as computer screens are two-dimensional surfaces. Our space behaves like a hypersphere surface so if it is generated, it could actually be so. A four-dimensional quantum network could create a three-dimensional surface that acts like our space, based on polar dimensions. Reverse engineering then suggests that our space is the surface of hyper-bubble expanding in the quantum bulk.
This conclusion explains why our space is expanding everywhere at once, not from a physical centre, as a linear space would. It also implies that our space is curved. Planets, stars, and galaxies are curved, so why not the universe? The earth was once thought flat because it seemed so, but now we know it isn’t, so is space the same? But if space is curved, why does it seem flat to us? One answer is that a hypersphere surface that has expanded for 14 billion years at the speed of light would seem flat to us, just as the surface of the earth once did. What else then does space as a hypersphere surface imply?