Transverse waves vibrate at right angles to their movement, but light moves in every physical direction so it can’t vibrate in our space. If light vibrated in a physical direction, it couldn’t move that way, so space wouldn’t be isotropic (the same in every direction). In simple terms, after space lets light move in three dimensions, there are no free directions for a transverse wave to vibrate into. Light then is a transverse wave that can’t vibrate transversely within our space.

However, if our space is a surface, then light could move on it as waves do on a lake, but in three dimensions not two. If light is a transverse wave vibrating outside our space, as complex number theory describes it, then we are 3D “Flatlanders”.
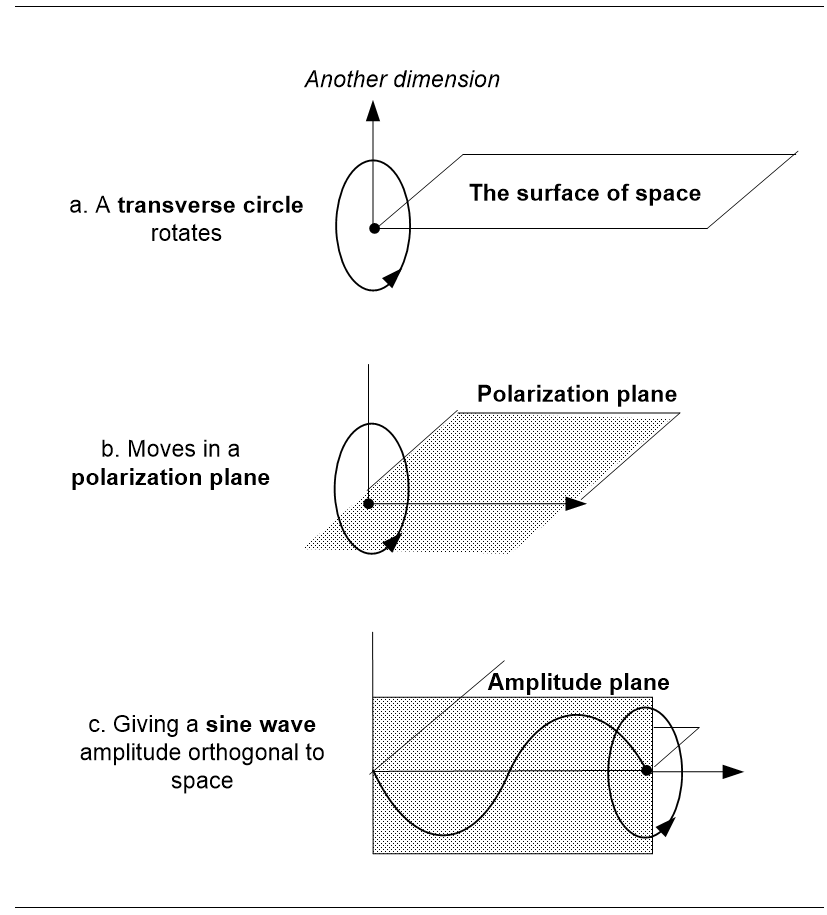
In Abbot’s story, Flatlanders were beings who lived their lives on a surface that had only two dimensions (Abbott, 1884), so they could see a circle but had to imagine a sphere. Now suppose a point entity moved on their land that set values in a circle at right angles to it (Figure 3.8a). Flatlanders could then explain it as a vibration in an imaginary plane, just as we explain light in complex number theory. As the point moves, it would trace out a sine wave with a frequency and a polarization plane in their space (Figure 3.8b), again as we have for light. They could then explain this moving point as an imaginary vibration, as we do for electromagnetism (Figure 3.8c).
Complex numbers then could explain electro-magnetism because light really does vibrate outside space, so:
“In quantum mechanics there really are complex numbers, and the wave function really is a complex-valued function of space-time.” (Lederman & Hill, 2004), p346.
Complex numbers describe light as rotating outside our space (Note 1), see Figure 3.9. Science calls this rotation imaginary because it doesn’t exist in our space, just as Flatlanders might call a rotation outside their space imaginary. But in their case, there really is a third dimension, so our case could be the same. If our space is a surface in a higher dimensional network, then light can vibrate into a fourth dimension as the equations say.
If our space is a surface inside a quantum network, then light can vibrate transversely. It can’t leave that surface, just as water waves can’t leave the surface of a pond, so if we are the same, we can’t leave our space. If so, we are three-dimensional Flatlanders, who call a vibration transverse to our space imaginary, but what vibrates when light does?
Note 1. Complex number theory describes a rotation into an imaginary plane. In normal multiplication, multiplying a number by two doubles it, e.g. 5 x 2 = 10. Multiplying by 4 adds it four times, e.g. 5 x 4 = 20. In complex multiplication, i is a 90° rotation into an imaginary plane, so times 2i is a 180° rotation that turns a number into its negative, e.g. 5 x 2i = -5. Times 4i is a 360° rotation that has no effect, so 5 x 4i = 5.