Does light vibrate in a physical direction? In physical realism, it must do so because space gives all possible directions. Sound is a longitudinal wave that vibrates air molecules in its travel direction, so there is no sound in empty space because there are no air molecules there. In contrast, light travels in the vacuum of space or we couldn’t see the stars at night.
It is a transverse wave, that vibrates at right angles to its line of travel but that can’t be a physical direction because space is isotropic so “up” from one view is “down” from another. Simply put, physical space has no “free” direction for positive-negative electromagnetic values to vibrate into so physical realism can’t explain how light vibrates at all.

Space as a surface however lets light move on space as waves move on a lake except this surface has three dimensions not two. Light then is a transverse quantum wave vibrating into a plane beyond our space, just as complex number theory describes, which this makes us 3D “Flatlanders”.
In Abbot’s story, the Flatlanders were beings who lived their lives on a 2D surface (Abbott, 1884). Everything they did happened in two dimensions not three, so they could see a circle say but could only imagine a sphere as expanding and contracting circles passing through their reality.
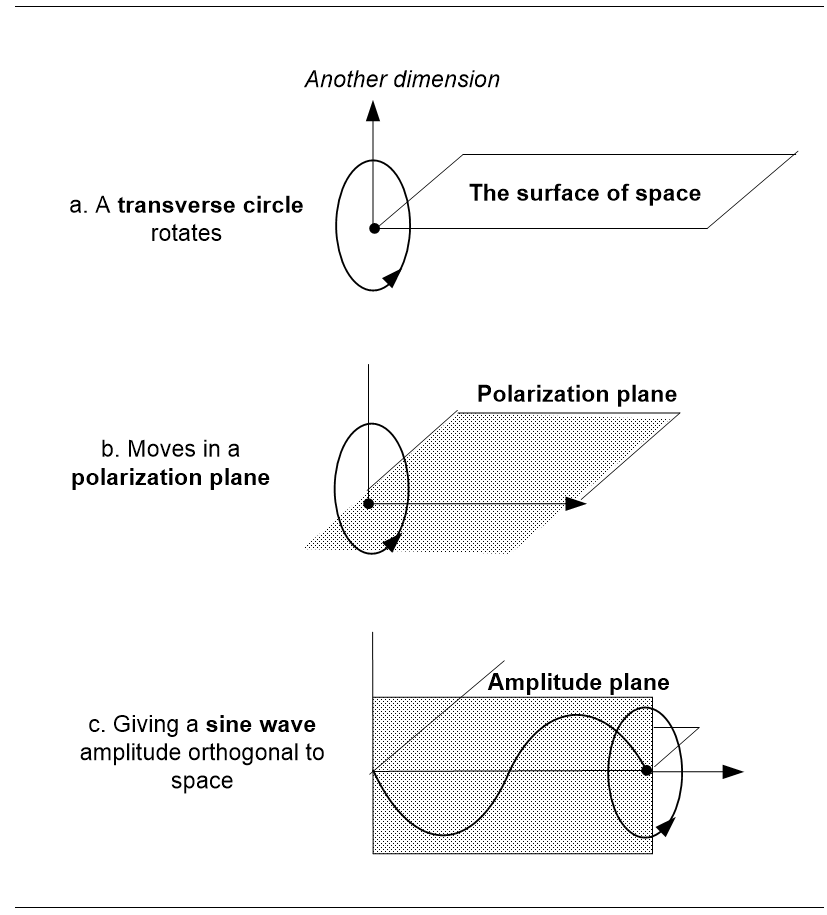
Now imagine a point moving on their flat land that sets values in a transverse circle at right angles to their space (Figure 3.8a). Flatlanders could only conceive of these values existing in a complex plane that didn’t exist for them, as we do for light. As the point moves, it defines a polarization plane in their space (Figure 3.8b), again as we have for light. To explain this, they might postulate an “unreal”, to them, sine wave amplitude (Figure 3.8c), just as we do for electromagnetism.
That light is a transverse rotation outside space suggests that complex numbers explain electromagnetism because light really is rotating outside space, so:
“In quantum mechanics there really are complex numbers, and the wave function really is a complex-valued function of space-time.” (Lederman & Hill, 2004) p346
Complex numbers describe a rotation into a dimension outside our space (Figure 3.9) that we call imaginary because it doesn’t exist in our space, just as Flatlanders might call a third dimension that doesn’t exist in their space imaginary. But that a dimension doesn’t exist in our space doesn’t mean it doesn’t exist at all if, like Abbot’s Flatland, our 3D space is contained within a higher dimensional space.
If our three-dimensional space exists within a quantum network with four degrees of freedom, light can vibrate into a dimension outside space. In simple terms, physical space is a surface within a four-dimensional quantum space. If our bodies exist as quantum waves that vibrate into a quantum space, we can’t enter that space any more than a water wave can leave the pond surface it vibrates on. It follows that we are three dimensional Flatlanders.