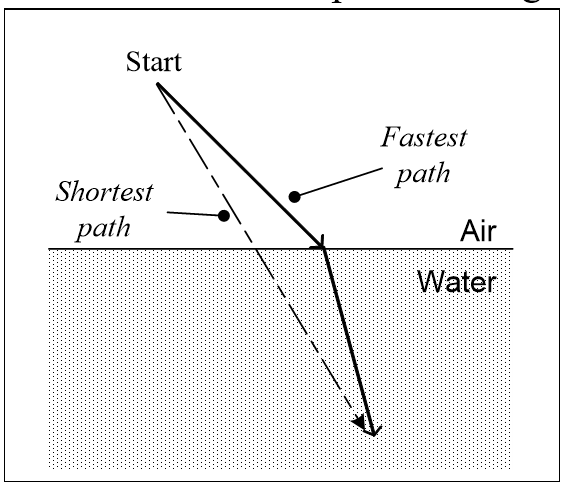
In 1662 Fermat amended Hero’s law to be the path of least time because when light enters water, where it travels slower, it refracts to take the fastest path not the shortest path. In Figure 3.15, light takes the path that bends as it enters water, not the dotted shortest path.
To understand this, suppose the photon is a lifeguard trying to save a drowning swimmer as quickly as possible. The fastest path to the swimmer isn’t the dotted straight line but the solid bent line because lifeguards can run faster than they swim, so it is faster to run further down the beach then swim a shorter distance. The dotted line is the shortest path but the solid line is the fastest, and that is the path light takes in Figure 3.15. But while a lifeguard might know in advance which path is fastest, how does refracting light know this?
In 1752, Maupertuis generalized further that:
“The quantity of action necessary to cause any change in Nature always is the smallest possible”.
Euler, Leibnitz, Lagrange, Hamilton, and others then developed the mathematics of this law of least action, that nature always does the least work, sparking a furious theoretical debate on whether we live in the best of all possible worlds. Despite Voltaire’s ridicule, how light always finds the path of least action, for any destination, remained a mystery.
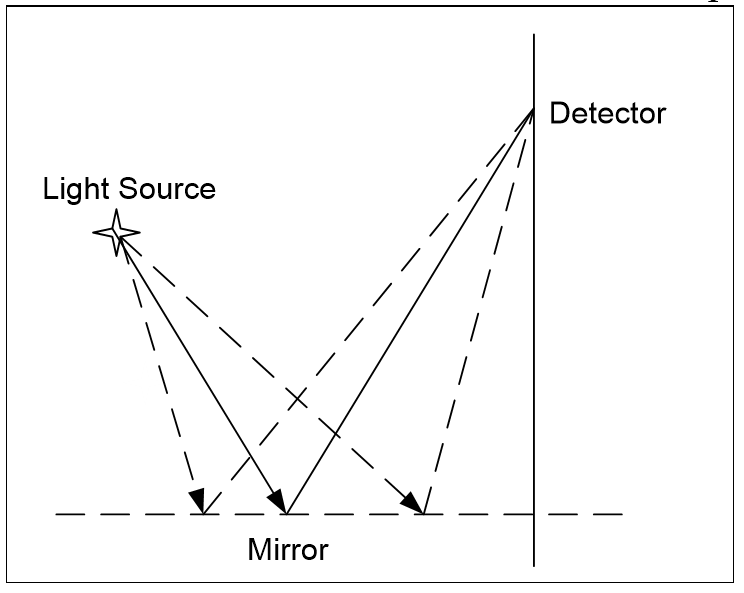
For example, light bouncing off the mirror in Figure 3.16 could take any of the dotted paths shown, but according to optics, always takes the solid line fastest path. But as a photon moves forward in time to trace out its path, how does it at each stage know the fastest route? As Feynman says:
“Does it ‘smell’ the neighboring paths to find out if they have more action?” (Feynman et al., 1977), p19-9.
To say that a photon chooses in advance the path of least action is to get causality backwards. That a photon, the simplest of all things, with no known internal mechanism, always finds the fastest path to any destination, for any media combination, any path complexity, any number of alternate paths, and inclusive of relativity, is simply miraculous. The law of least action is a physical law that is no less a mystery today than it was centuries ago, but like all physical laws, it has its basis in a quantum law.