Quantum spin is so strange that when Pauli first proposed it, he wasn’t believed:
“… the spin of a fundamental particle has the curious feature that its magnitude always has the same value, although the direction of its spin axis can vary…” (Penrose, 1994), p270.
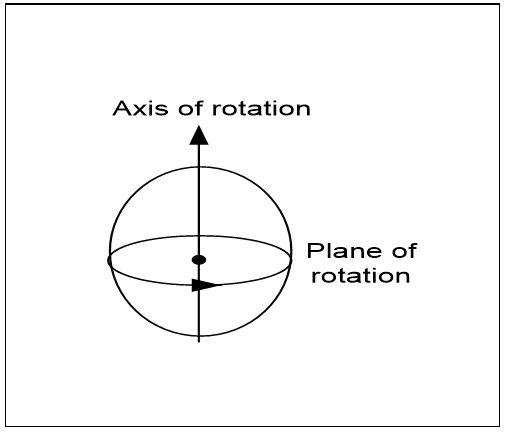
A physical particle spins in a rotation plane around an axis of rotation (Figure 3.17), so its axis must be known to measure its spin. Measuring spin on an axis that isn’t its rotation axis gives less than the total spin. If the spin axis is unknown, one must measure spin on three orthogonal axes to get the total spin. In contrast, the spin of a quantum entity measured on any axis is always the same, so quantum spin doesn’t work like physical spin.
In this model, detecting a photon’s spin on any axis gives all its spin for the same reason that detecting it always gives all its energy. In both cases, a physical event, is an all or nothing restart of the photon, including all its energy or spin, so this property is expected.
Physics measures quantum spin in units of Planck’s constant in radians (Note 1). If Planck’s constant represents the linear transfer of one Planck process, as proposed earlier, Planck’s constant in radians will then represent its units of angular transfer, or spin, so this is also expected.
Finally, according to quantum theory, quantum spin occurs in both directions at once, so measuring it gives either spin direction randomly. Just as a photon goes through two slits at the same time but is randomly in one or the other, so it also spins both ways and is randomly either. It follows that the quantum law of all action applies to rotational movement as well as linear movement, so a photon that can travel through two slits at once can also rotate in two directions at once. The measured spin result is then random because it depends on which instance accesses the server first, so this property of quantum spin is also expected.
Spin is then a fundamental property of every quantum entity because processing spreads in angular as well as linear directions, and its properties are as expected.
Note 1. Quantum spin is defined as Plank’s reduced constant ħ = h/2p (in angular radians).