Polarization is the property of a transverse wave that describes its vibration direction, so that light can polarize suggests that it is a wave. But if a filter that blocks a ray of polarized light is turned a bit, a few photons get through at full strength, and its angle decides how many photons do that. Yet turning an obstacle that blocks wave should weaken it as a whole, not let some waves through and others not, which is how particles would behave. Why then in this case, does light act like it is made of particles?
The answer lies in the nature of quantum spin. If this spin occurs, it will have a:
a. Rotation axis. Around which the spin occurs, and a
b. Rotation plane. In which the spin rotation occurs.
How then does a photon spin? Let us suppose that it spins on its movement axis, as a bullet does, so it rotates into the planes that cut that axis (Figure 3.19). Oddly enough, this spin won’t alter its polarization because it vibrates outside our space.
To understand this, consider a book sitting on its edge on a table. If the book spins in the rotation plane of the table, its height doesn’t change because it is at right angles to table. Hence, if the table surface is our space, a photon spinning in in our space doesn’t change its transverse vibration height. A photon that spins in our space doesn’t change its polarization because its vibration direction doesn’t change (Note 1), so its polarization plane doesn’t change either.
Now consider a filter that blocks light polarized one way. As it turns, more and more light gets through until eventually it all does. Why then does turning a filter have an effect but turning a photon doesn’t? In table analogy, the book represented a photon moving in some direction across the table surface, whose vibration amplitude was the book’s height. Spinning the book then didn’t alter either its height or its movement direction. But if the filter is like a thin wall that stops movement on the table when it is face-on, turning it will block the photon less. Turning a filter is like turning a wall on the table to obstruct a wave less (Note 2), while turning a photon in our space doesn’t alter its wave amplitude or direction. Of course it isn’t that simple, as in Chapter 4, matter fills many quantum directions not one, but the principle still applies.
Why then do some photons pass entirely through a filter on an angle? Again, it is because a physical event is an all-or-nothing affair. The filter reduces the probability that instances get through, but if one is detected, the entire photon restarts there. By the same logic, what passes through the filter is also an entire photon. A photon then travels like a wave because it is a wave, but is detected like a particle because processing always restarts completely.
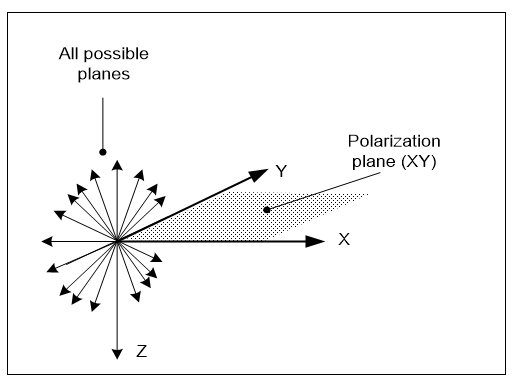
Note 1. Let the photon’s wave amplitude be in a direction Q, at right angles to its polarization plane XY. Now if the photon spins in the plane YZ, this swaps its Y and Z values but leaves Q unchanged, as it is at right angles to that spin. It follows that a photon can spin around its movement axis X without altering its amplitude vibration, and hence its polarization plane.
Note 2. If Q is the quantum amplitude it reduces as Q.Cos(q°), where q° is the angle between that amplitude and the filter direction in quantum space, so at a 90° angle it has no value, as Cos (90°) = 0.