The above explains what happens when light meets a filter on an angle. Experiments show that a filter at an angle to the polarization plane of light reduces the light that gets through but still lets some photons through entirely. A filter at bigger angle to the light polarization lets fewer photons through, so a filter at 81º to the polarization plane lets only 10% of the photons through but some still get through entirely. How can a photon pass entirely through a filter that mostly blocks it? The answer now proposed is that quantum spin works in four dimensions.
To recap, spin in general involves a:
a. Rotation axis. Around which the spin occurs.
b. Rotation plane. In which the spin occurs.
Imagine a spinning propeller that rotates round an axis into the rotation plane that we see from the front. From the front, the blades rotate into the vertical and horizontal but the axis is just a point. From the side, the axis line is seen but the blade “disappears” as it spins into an unseen depth dimension.
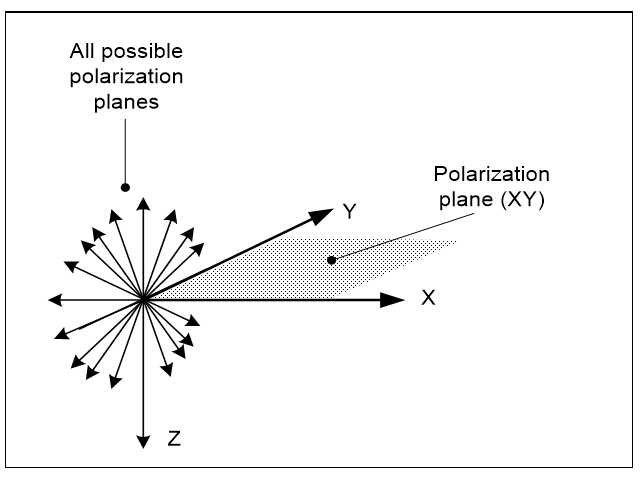
Spin in four dimensions works like spin in three but with more options. If a photon spins on its movement axis as a bullet does, it spins into all the planes that cut its movement axis (Figure 3.19). This allows it to pass through a filter on an angle to its polarization plane. But as it spins, its quantum amplitude direction doesn’t change because it isn’t on the rotation plane (Note 1). So when a vertically polarized photon spins into the horizontal plane it disappears entirely, like a piece of paper on edge that can’t be seen. As a photon spins on its movement axis, its amplitude varies according to angle. The quantum amplitude of a spinning photon appears and disappears like a propeller seen from the side. Some light gets through a filter on an angle because its amplitude projects into the planes that cut its movement axis according to angle (Note 2).
Why then do some photons pass entirely through a filter on an angle? Again, it is because physical measurement is an all-or-nothing affair. The filter reduces the probability that instances get through a filter but if one does and is detected, the entire photon restarts at the point. The entire photon gets through a filter for the same reason that a screen point registers the entire photon. A physical event always delivers “the photon” because it restarts all the quantum processing that is the photon.
Note 1. The Planck transverse circle already turns around the X axis into the YQ plane, but the photon can still spin in the YZ plane. This swaps its Y and Z values while leaving Q and X unchanged. Q remains perpendicular to XY, so as Y and Z swap it becomes invisible, as it has no extension orthogonal to the XZ plane.
Note 2. If Q is the quantum amplitude it reduces as Q.Cos(q°) as it spins, where q° is the angle from the polarization plane. So at a 90° angle it has no value as Cos (90°) = 0.