Heisenberg’s uncertainty principle is that one can’t know both the exact position and momentum of a quantum entity at the same time. Physics calls these facts complementary, i.e. separately knowable but jointly unknowable. This isn’t expected of a particle but quantum theory insists that measuring either property denies all knowledge of the other entirely. To understand this, consider that every measurement is an information transfer:
“… a measuring instrument is nothing else but a special system whose state contains information about the “object of measurement” after interacting with it:” (Audretsch, 2004), p212.
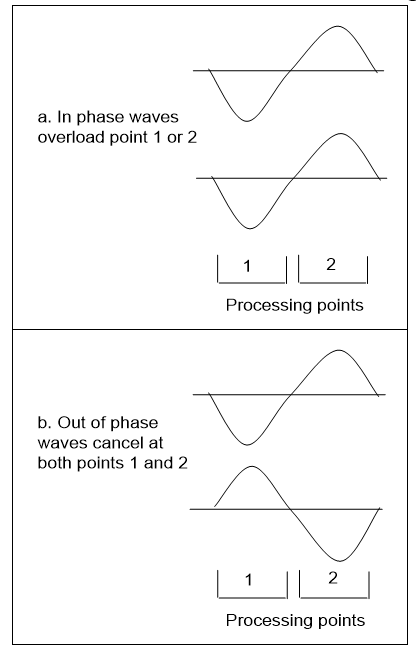
Now if every measurement is physical event triggered when quantum waves interact, it is one wave gaining information from another. Figure 3.25 shows a simple case of two waves interacting over two points of space that can combine to overload two ways:
a. If they are in phase, one point can overload, to give an exact position, but no length information is provided.
b. If they are out of phase, both points cancel to give an exact wave length, but no position information is provided.
It follows that a known wave interacting with an unknown one can reveal position or wavelength but not both, with no repeats. If the result gives a position, there is no wavelength data and if it gives a wavelength, there is no position data. In both cases, the observed wave has given all the information it can to the interaction. One wave observing another can give position or length but not both, and since length is needed to define momentum, this equates to the uncertainty principle.
The uncertainty principle follows from the nature of wave interactions, based on De Broglie’s equation (Note 1). In this model, Planck’s constant represents a core network process that no information transfer can be less than, so the change in position plus momentum can’t be less than Planck’s constant (Note 2). The uncertainty principle then reflects how waves based on a core process interact.
Note 1. If p is momentum, λ is wavelength and h is Planck’s constant, then p = h/ λ
Note 2. Mathematically δx.δp ≥ ħ/2 where x is position, p is momentum and ħ is Plank’s constant in radians.