Heisenberg’s uncertainty principle is that one can’t know both the exact position and momentum of a quantum entity at the same time. Physics calls these facts complementary, as they are separately knowable but jointly unknowable. This isn’t expected of a particle but quantum theory insists that measuring either property denies all knowledge of the other entirely.
To understand this, consider that every measurement transfers information:
“… a measuring instrument is nothing else but a special system whose state contains information about the “object of measurement” after interacting with it:” (Audretsch, 2004), p212.
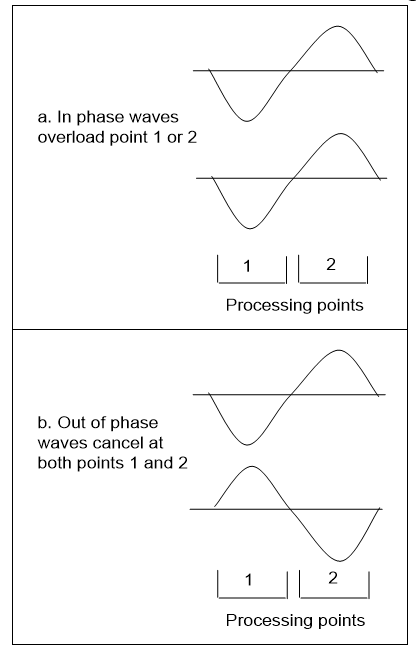
Now if every measurement is physical event, triggered when quantum waves overload a point, a measurement is one wave gaining information from another. Figure 3.25 shows a simple case of two waves interacting over two points of space. They can then combine to overload a point in two ways:
a. If they are in phase, one of the points can overload to give a position exactly, but no length information is provided.
b. If they are out of phase, both points overload to give an exact wavelength, but no position information is provided.
It follows that a known wave interacting with an unknown one can reveal a position or its wavelength, but not both, with no repeats. If the result gives a position, there is no wavelength data and if it gives a wavelength, there is no position data. In both cases, the observed wave has given all the information it can to the interaction, so one wave observing another can give position or wavelength, but not both. Since length is needed to define momentum, this is equivalent to the uncertainty principle.
The quantum uncertainty principle follows from the nature of wave interactions, based on De Broglie’s equation (Note 1). In this model, Planck’s constant represents a core network process that no information transfer can be less than, hence the change in position plus momentum can’t be less than Planck’s constant (Note 2). The uncertainty principle then just reflects how processing waves with a core process interact.
Note 1. If p is momentum, λ is wavelength and h is Planck’s constant, then p = h/ λ
Note 2. Mathematically δx.δp ≥ ħ/2 where x is position, p is momentum and ħ is Plank’s constant in radians.