The measurement problem in physics is that while Schrödinger’s equation determines how quantum waves evolve, how they collapse when measured is indeterminate. How then do many indefinite quantum states instantly become one definite physical state? This problem was raised early last century and no progress has been made on the matter since:
“The history of the quantum measurement paradox is fascinating. There is still no general agreement on the matter even after eighty years of heated debate.” (Laughlin, 2005), p49.
Essentially, we understand how quantum waves spread but not how they collapse, and but for this problem they could be real, as after all:
“… why not simply accept the reality of the wave function? (Zeh, 2004), p8.
This didn’t happen because the measurement problem means that quantum theory:
“… paints a picture of the world that is less objectively real than we usually believe it to be.” (Walker, 2000), p72.
In other words, what quantum theory describes makes no sense so it can’t be real. Quantum collapse is part of quantum theory, so it can’t just be ignored. If the wave part of quantum theory is accepted as real, then the jump of quantum collapse must be the same:
“… if we are to take y [the quantum field] as providing a picture of reality, then we must take these jumps as physically real occurrences too…” (Penrose, 1994), p331.
Schrödinger tried to explain the quantum field but failed, as did all who came after him, because its waves superpose in physically impossible ways, entangle to ignore the speed of light limit, and instantly collapse to a point when observed, but:
“How can something real disappear instantaneously?” (Barbour, 1999), p200.
When Pauli and Born defined the quantum field as the probability that a physical event will occur, physics inevitably became about what wasn’t physical, so:
“For the first time in physics, we have an equation that allows us to describe the behavior of objects in the universe with astounding accuracy, but for which one of the mathematical objects of the theory, the quantum field y, apparently does not correspond to any known physical quantity.” (Oerter, 2006), p89.
The measurement problem, that quantum waves act in an impossible way when measured, then produces the paradox that quantum unreality causes physical reality, but as one physicist notes:
“Can something that affects real events … itself be unreal?” (Zeh, 2004), p4.
The quantum states that predict physical states are physically unreal, so as Penrose says:
“How, indeed, can real objects be constituted from unreal components?” (Penrose, 1994), p313.
The quantum paradox is that if unreality causes reality, what doesn’t exist causes what does, which is illogical. If one thing causes another, how can a real effect have an unreal cause? Given a cause and effect, if only one is real, surely it is the cause not the effect?
For over a century, physics has faced this paradox like a deer in headlights, blinded by the brilliance of quantum theory, but stuck in the orthodox stance of materialism. This situation hasn’t changed for a hundred years, so if nothing is done, the next hundred years will be the same.
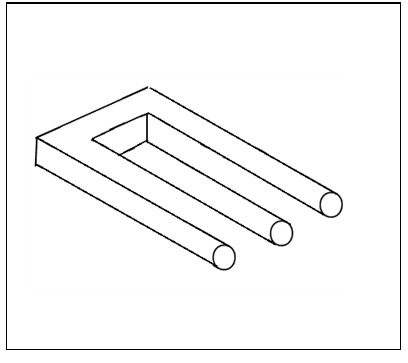
Yet paradoxes are usually based on false assumptions. For example, the object in Figure 3.26 seems to have two square and three round prongs, based on where you look. If you look at the top, there are two square prongs, but if you look at the bottom, there are three round ones! Both seem to be true, producing the paradox that one object has two and three prongs, which is impossible! The answer isn’t to invent some sort of square-round duality, but to recognize that the same line can’t bound both a square and a round prong at the same time. When this false assumption is exposed, the paradox ceases to exist, because it is just an illusion.
Likewise, the quantum paradox, that unreal quantum events cause real physical events, is based on the false assumption that physical things constantly exist and so aren’t generated. The answer to this paradox isn’t to invent a wave-particle dualism that institutionalizes its illogic but to expose the fallacy behind it, of materialism. If matter doesn’t constantly exist, the quantum paradox disappears because physical events can now be generated. This is possible because processing waves on a network can spread, superpose, collapse and restart, just as quantum theory describes. Quantum realism is that physical events are generated by quantum events, rather than the other way around.