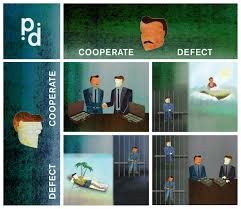
Game theory is the systematic study of the “rational” choices of individuals in social interactions. It presents the essentials of social situations for analysis and underlies many economic, political and management theories. Yet its validity was challenged by the discovery of a scenario called the prisoner’s dilemma.
In the prisoner’s dilemma, two prisoners (Bill and Bob) each face two-year jail terms on circumstantial evidence for a crime they did commit. Each is separately offered a plea bargain, to testify against the other. If the other does not testify, he walks free but his partner gets seven years in jail. If both testify, both get six years (one off for testifying). In outcome utility terms the options are:
1. Bill and Bob stay silent and each gets two years in jail.
2. Bill confesses for immunity and Bob gets seven years.
3. Bob confesses for immunity and Bill gets seven years.
4. Bill and Bob both confess and both get six years jail.
Table 5.1 shows the outcome payoff matrix as free years out of seven. If both cooperate and keep quiet, both get five free years, but if both defect and testify they only get one free year each. The temptation is for one to defect and get seven free years, while the other cooperating sucker gets none. As individuals following Rule 1, each prisoner concludes:
• Whether the other person cooperates or defects doesn’t depend on my choice.
• If he defects, it pays me to defect, as then I get 1 not 0 free years.
• If he cooperates, it still pays me to defect, as I get 7 not 5 free years.
|
Years free(Bill/Bob) |
Bob |
||
|
Cooperate |
Defect |
||
|
Bill |
Cooperate |
5/5 |
0/7 |
|
Defect |
7/0 |
1/1 |
|
Table 5.1. Prisoner’s dilemma—Individual outcomes
Game theory concludes that rationally it always pays individuals to defect, as the expected defect average gain is 4 but the cooperate average is only 2.5. If both parties follow game theory’s Rule 1, defect/defect is the equilibrium state. People rationally maximizing profit creates the worst possible result for all!
However working as a social unit following Rule 2, gives a different result. The available social acts for the pair are mutual cooperation and mutual defection with expected gains of 10 and 2 respectively (Table 5.2). If both parties follow Rule 2, mutual cooperation is the new equilibrium state. So when social cohesion is allowed, simulated agents in a prisoner’s dilemma situation evolve a cooperative equilibrium (Dayton-Johnson, 2003).
In performance terms, Rule 1 gives 2 free years of value while Rule 2 gives 10 free years, a considerable net gain. Game theory assumes that rational beings must calculate payoffs for the individual, but it is just as rational to calculate payoffs for the social unit as a whole (Table 5.2). After all, Rule 2 is just Rule 1 applied to the social unit instead of the individual unit. It is just as logical and just as pragmatic.
Conversely, it is illogical to label alternatives to individual self-interest irrational if they generate more value, given that we ourselves are a society of cells, and cancer is the result when one of them acts for itself alone regardless of the rest. Since what people define as “self” often includes the community around them (Persky, 1995), both rules are equally rational and pragmatically grounded.
Table 5.2. Prisoner’s dilemma—Social outcomes
|
Years free (Pair) |
Social Outcome |
|
|
Social Act |
Cooperate |
10 |
|
Defect |
2 |
|