In the standard model, an electron particle exists at a point so it occupies no space, but how can it then have mass? The mass of a particle should come from its substance, but a particle with no size can’t have a substance. The idea that electron particles have mass but no size seems seriously flawed. But if an electron is processing in some form, as light was in the last chapter, it can exist at a network point that, like a screen pixel, occupies a space but can’t be divided.
Our networks also transfer data by communication channels. Each channel handles different data, just as different TV channels handle different shows. If the quantum network is the same, when light passes through a point in space, each photon is handled by one channel. A point then has a channel for each photon polarization, so there are many channels per point. And as our channels are mostly duplex (they work in both directions), we expect the same here. Finally, each channel has a finite bandwidth, which in this model is the quantum process defined earlier (3.3.1).
Based on the logic of processing, each channel of a point of space can:
1. Accept one photon with one polarization coming from one direction.
2. And at the same time accept a photon with the same polarization from the opposite direction.
3. Up to a bandwidth of one quantum process per cycle.
One channel is then represented by a line through a point, plus a plane cutting it to represent the polarization it accepts. Hence, if two photons with the same polarization enter a point from opposite directions, one channel can handle both, up to its bandwidth of one quantum process. Since each photon is a quantum process spread over many points, light rays in general don’t collide, as is observed.
Yet this model suggests an exception. One photon is one quantum process spread over its wavelength, and the channel bandwidth is also a quantum process, so dilute photons don’t overload it. But if very high frequency photons that divide over only two points meet, they will overload the channel. Each photon presents half a quantum process, so two of them meeting head-on in a channel will overload its one process bandwidth. Note that this wavelength of two Planck lengths is the shortest possible, as a photon at one point is empty space. An extreme photon distributed over two network points runs half a quantum process at each, so two of them meeting will overload the channel bandwidth of one quantum process. Instead passing through each other, extreme photons that meet head on will collide in a physical event!
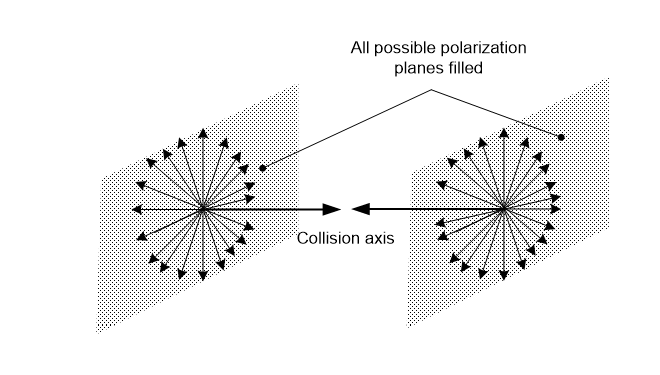
Yet photons spin on their movement axis, so this event will just restart them in other channels, but what if every channel overloads? If rays of light with extreme photons in every polarization plane meet head-on at a point, every channel on one axis will overload at the same time (Figure 4.2). There are no free channels for the photons to carry on, so they will restart at that point. This result seems unlikely but extreme light was common in the first plasma, so by the law of all action, that what is possible will happen (3.6.3), it had to occur.
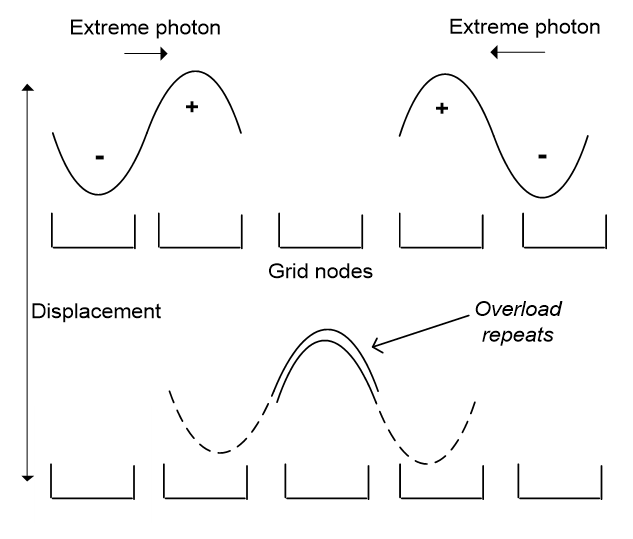
Figure 4.3 shows the result for one channel, with every channel the same. Now let a photon head be its leading half, and its tail be its following half. Two heads, each of half a quantum process, overload the channel bandwidth of one, so both photons restart next cycle. Two new photons then set off in opposite directions from the same point, but they again collide in another overload that restarts them again. This recurring overload repeats every cycle because every channel is the same. The network that once hosted only waves now has a constant processing bump, which is an electron.
The result is stable, because any photon arriving on that axis finds all the channels taken, while a photon arriving at right angles passes through it using different channels. An electron is then a repeating overload, like a stuck record that keeps repeating the same song.
Is this repetition possible? In experiments, electro-magnetic waves can repeatedly interact to form static states (Audretch,2004, p23), as frequent observations maintain the quantum state if the time delay is short (Itao,Heizen, Bollinger, & Wineand, 1990). Feynman’s PhD partitioned the electron wave equation into opposing advanced and retarded waves, but he didn’t pursue it. Other theories that let waves oppose include Wheeler–Feynman’s absorber theory, where retarded and advanced waves give rise to charge (Wheeler & Feynman, 1945), Cramer’s transaction theory also based on retarded and advanced waves (Cramer, 1986), and Wolff‘s suggestion that electrons are in and out spherical waves (Wolff,M.,2001). If electro-magnetic waves form standing waves as other waves do (Figure 4.4), an electron could be a standing wave created when extreme photons collide.
This conclusion contradicts the standard model in several ways. Instead of a particle of matter with no size, which makes no sense, an electron now occupies a quantum network point that has a size, just as a screen pixel does. Instead of having no structure, an electron is now a one-dimensional collision. Instead of matter being an inert substance, it is now light pulsing constantly in a never-ending loop. Matter is now frozen light, a standing wave of light that seems static but being light, is always active. Yet as this result only applies to one axis, an electron is just one-dimensional matter.
When a computer hangs in an infinite loop that a restart can’t fix, it is a glitch, but for the quantum network, the matter glitch was an evolution not an error.