To reverse engineer space, its properties must be known. If space is nothing at all, as Leibniz thought, it has no properties, but nothing at all can’t expand as our space does. If space is something, it must have properties, which by the previous sections, are that it is:
- Discrete. Made of points with a minimum size.
- Directional. Its points allow finite directions of movement.
- Three dimensional. It has three degrees of movement freedom.
- Finite. It isn’t infinitely large in size.
- Expanding everywhere. It isn’t expanding from an origin point within itself.
- Scalable. Doesn’t change as it expands, as far as we can tell.
Our space can’t be Cartesian because it isn’t expanding from a point within itself, yet linear space is so deeply ingrained in western thought that some think it is the only way a space can be, but it isn’t. Euclid derived his coordinates by extending a point in a straight line, then extending another line at right angles to get a plane, then repeating to get a volume, but mathematics also lets us extend a point by rotations, to derive polar coordinates (Note1).
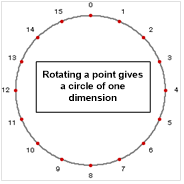
A polar space also begins with a point, as before, but this time it needs extension to stand alone, as a point of no extent can’t exist. The first dimension then arises from a rotation around that point, to give a circle, whose circumference represents a dimension of points (Figure 2.3). This dimension has two directions, as each point connects to two neighbors. The distance between points is the number of connections between them, so points 1 and 2 in the figure are close, but points 1 and 10 are far apart. The circle is also finite, and it can expand indefinitely from a point that isn’t on itself (the circle center).

Then, just as Euclid extended a line, a circle can extend by orthogonal rotation to give a sphere whose surface has two dimensions (Figure 2.4). Again, as the sphere expands, its surface increase everywhere at once, not from a point on itself. This matches how cosmologists say our space expands, which is like a ballon surface, for as Hoyle said:
“My non-mathematical friends often tell me that they find it difficult to picture this expansion. Short of using a lot of mathematics I cannot do better than use the analogy of a balloon with a large number of dots marked on its surface. If the balloon is blown up the distances between the dots increase in the same way as the distances between the galaxies.” (Hoyle, 1950).
Our space expands everywhere at once, like the surface of a balloon being blown up, so a two dimensional being living on such a surface would see a space that is discrete, directional, finite, and increasing everywhere, just like our space, but with two dimensions instead of three. To a reverse engineer, this suggests that our space is polar not linear, but is a three-dimensional polar space possible?
Note 1: Cartesian coordinates are represented by (x, y, z) values, but polar coordinates are represented by (r, a, b), where r is the radius from a fixed point, and alpha and beta are angular directions. Both systems need a (0,0,0) point.