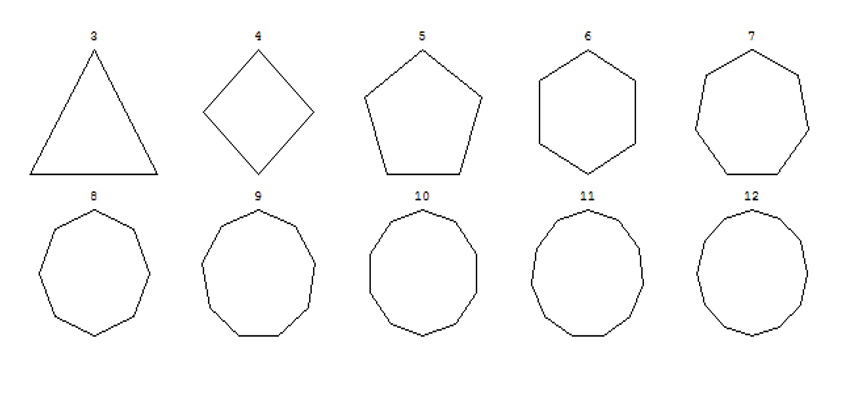
In the derivation of polar space, the number of steps in each rotation is finite, so it is a discrete rotation. A discrete rotation must have a finite number of steps, so a triangle is made by three rotation steps, a square by four, a pentagon by five, and so on (Figure 2.6), where these N-rotations approximate a perfect circle as N increases. More rotation steps seem better because they allow more interaction directions, but wargamers use hexagons not octagons because a board of octagons has gaps in it. Hexagons fill the surface completely but octagons don’t, so the former are preferred.
In general, a rotational space based on a large N, as expected here, will have gaps in it, so not all paths will be reversible. Taking a route in reverse might not return to the exact same point, though it would be a true vicinity. A polar space with holes in it would allow particles to pass right through each other! Does this property then exclude a discrete polar space from describing our space?
It might seem so, but quantum theory describes quantum entities as probability clouds not billiard ball particles. When these clouds collide, they overlap an area, so a space with a few holes in it doesn’t matter. If quantum entities are probability clouds, a polar space with gaps in it still works.
For a polar space, the circle of neighbors around a point will be a finite number N, so it will have that many transfer connections. If each connection is a direction, this predicts that a point in space has a finite number of directions, so direction, like length, will be quantized, as a minimum Planck angle [Note 1]. Experiments with high frequency light could test wheter quantum events have a minimum Planck angle.
[1] If a point has N neighbors in a circle around it, the minimum Planck event angle is 360°/N.