How light travels to a destination depends on whether it is a wave or a particle. Newton explained why he rejected Huygens’s wave view of light as follows:
“For it seems impossible that any of those motions … can be propagated in straight lines without the like spreading every way into the shadowed medium on which they border.” (Bolles, 1999), p192.
He was correct that if light moves as a wave, it should bend round corners as sound waves do, but actually it does. In 1660 Grimaldi found that light does bend but less than sound because its wavelength is shorter. The question is then, how can a spreading wave travel in a straight line?
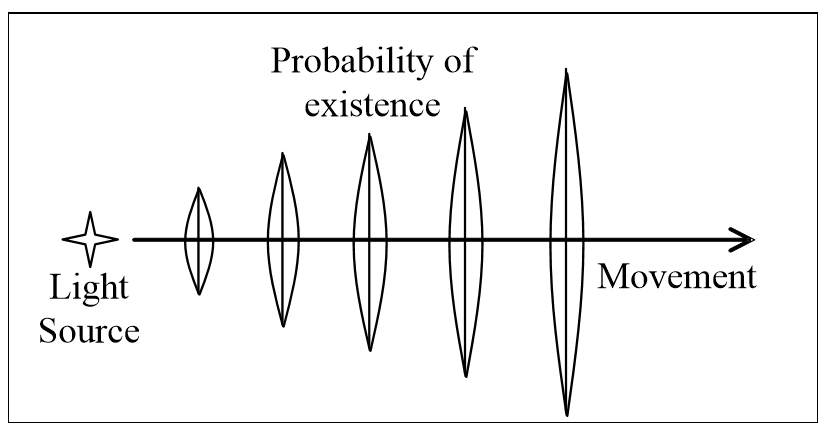
According to quantum theory, where a photon is detected depends on the power of its wave. Figure 3.13 shows how that power varies along its direction axis, where it’s more likely to exist at the thicker sections.
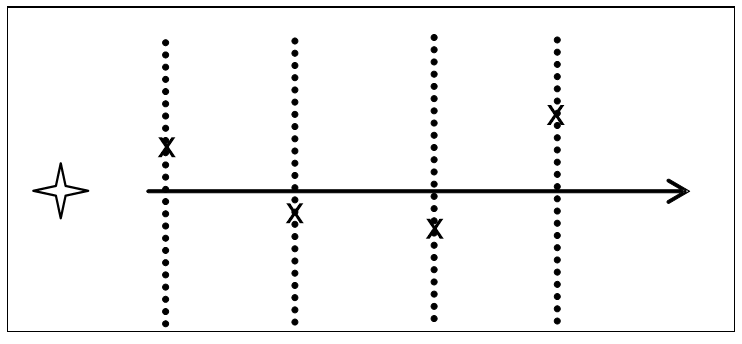
Detecting photons by screens at different distances confirms this, as the results aren’t a perfect straight line but randomly spread about (Figure 3.14). A physical particle would have to travel in a zigzag path to explain this! When a photon moves, it is most likely to exist in a straight line, but the wave itself spreads in all directions.
If light only travels in a straight line on average, why are the straight lines of Greek optics so effective? The answer isn’t because light consists of particles that travel in straight lines, but because it is a wave, but first, we continue the history of how light travels.