In the standard model, quarks are fundamental point particles, unrelated to electrons or neutrinos. They come in two types, called up and down, with different charges. An up quark has a plus two-thirds charge, and a down quark has a minus one-third charge. This lets two up quarks and a down quark combine into a positively charged proton that form the nucleus of Hydrogen, the first element of the periodic table. Each new periodic table element has one more proton plus some neutrons that arise from one up quark and two down quarks. Quarks form the protons and neutrons in the nuclei of all known atoms.
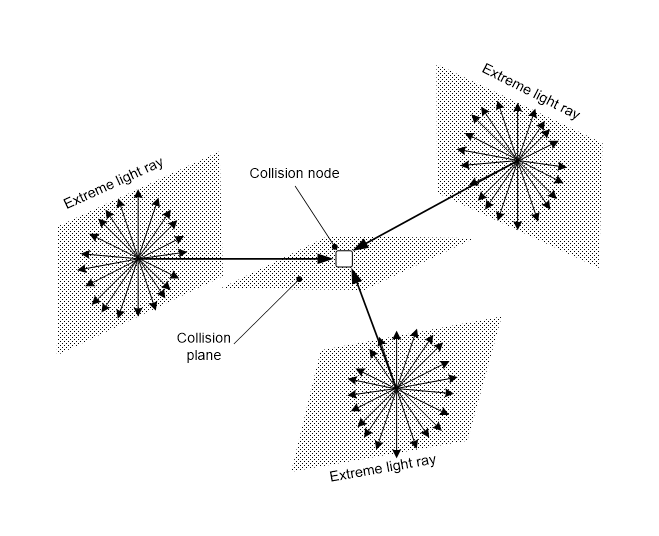
If an electron’s mass comes from a one-axis collision of extreme photons, quark mass must also arise in same way. The last section covered all the ways photons can collide on one axis, so a quark can’t be a one-axis result, but it could be a three-way interaction. If three rays of extreme light meet at a point, they must be on the same plane, as shown in Figure 4.9. Again, such an event is unlikely but again, it must have occurred in the early plasma by the quantum law of all action.
A three-axis collision has an interesting symmetry, as photons on any axis half exist on the other two by the cosine rule, so any quark axis is one ray vs. two others at half strength, which is a lepton type collision. But applying this feature to one axis doesn’t leave enough light to do the same to the other two.
It follows that this extreme light interaction isn’t stable alone, but physics tells us that unlike electrons, quarks are so unstable that they never exist alone. Had it not been so this model would fail, as few other reverse engineering options exist, but could quark processing fill all the channels of a plane through a point, just as electrons did for a line through a point?