The first atom, Hydrogen, is one proton and one electron, and the next, Helium, has two protons and two electrons but its nucleus also has two neutrons, and no-one knows why. Each higher element adds not just another proton and electron, but also one or more neutrons, so:
“… all the stable nuclei have more neutrons than protons (or equal numbers), and the heavier nuclei are increasingly neutron-rich.” (Marburger, 2011), p254.
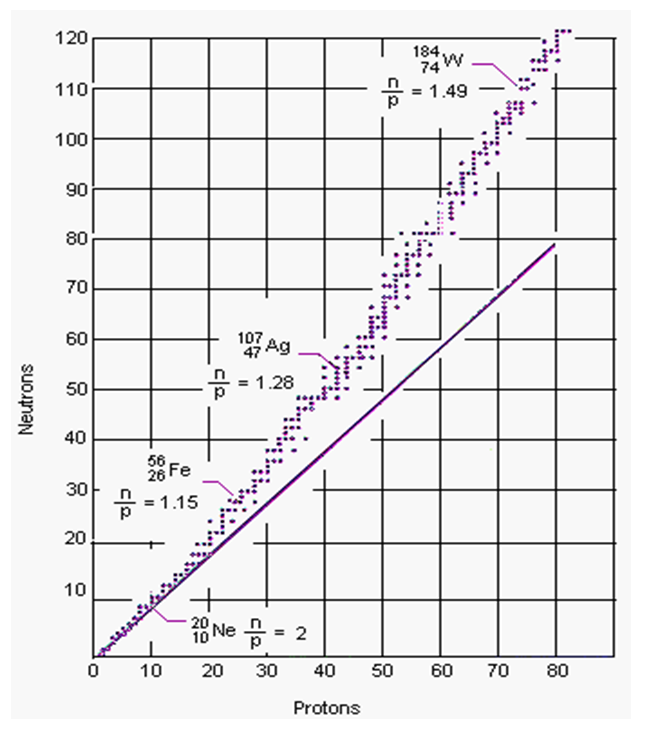
Current theories don’t explain why most nuclei need neutrons to be stable (Figure 4.22). The shell model of electrons doesn’t work, because some nuclei aren’t spherical. The standard model doesn’t help because if gluons hold the protons together, why are neutrons needed? That the nucleus is protons and neutrons sitting side-by-side like fruits in a bowl also predicts nothing. However if a proton is a closed quark triangle bound by photon sharing, that triangle can open up and recombine in bigger closed string that satisfies the same rules, namely a closed string with the internal angles of an equilateral triangle.
The Helium nucleus of two protons and two neutrons is then one quark string held together by photon sharing, so it has a unity that particles in a bowl don’t have. In the fruit-bowl model, a Helium nucleus is four proton or neutron particles glued together by gluons but in this model, it is single quark string where each link bends the string 60º until it connects back to its base. Higher nuclei can then form in the same way.
This explains why higher nuclei need neutrons. Positive protons can’t easily come side-by-side to share photons because they repel, so neutrons are needed as buffers. When the nuclear string forms, neutrons act as buffers between same-charge protons, which requires at least as many neutrons as protons, as observed (Figure 4.22). For example, a Helium nucleus of two protons needs two neutron buffers between the protons to form a closed string.
Closed quark strings will be compact and nearly spheres, as observed, but large nuclei may need more neutrons to avoid fold-back loci that happen to make protons adjacent. This also explains why some nuclei are more stable:
“Nuclei with either protons or neutron equal to certain “magic” numbers (2, 8, 20, 28, 50, 82, 126) are particularly stable.” (Marburger, 2011), p253.
Atomic nuclei as closed quark strings will fold in space to form shapes as proteins do, so the nuclei with magic numbers are just those that produce symmetric shapes that are more stable.
The quark string model explains what a fruit bowl model doesn’t, namely why nuclei need neutrons as well as protons, why some need more, and why some nuclei are more stable.