The periodic table organizes the elements of matter based on electron shells. Each row of elements represents an electron shell that ends when it is full with an inert atom like Neon. Neon doesn’t swap electrons with other atoms because its outer shell is full, but other atoms do. In every chemical reaction, from acidity to oxidation, atoms exchange electrons to complete their outer shell. Stable molecules form when atoms with extra electrons donate them to those with a deficit, in chemical bonds that complete their electron shells.
The current description of electron shells is based on two quantum numbers:
1. Shell n (1, 2, 3 …). Initially the orbit radius.
2. Sub-shell l (s, p, d …). Has no agreed meaning.
The shells and sub-shells deduced from spectroscopic analysis are shown in Table 4.7, where the sub-shells s, p, d, f, g, and h contain 2, 6, 10, 14, 18, and 22 electrons respectively. Bigger shell orbits fit more electrons, so doubling the first orbit quadruples its area to allow eight electrons, tripling it allows eighteen, quadrupling it thirty-two, and so on. Electrons then added to atoms based first on shells, inner before outer, then on available sub-shells, again in order. Hence, the periodic table first row has two elements, and the second row has eight elements, Lithium to Neon, but then there was a problem.
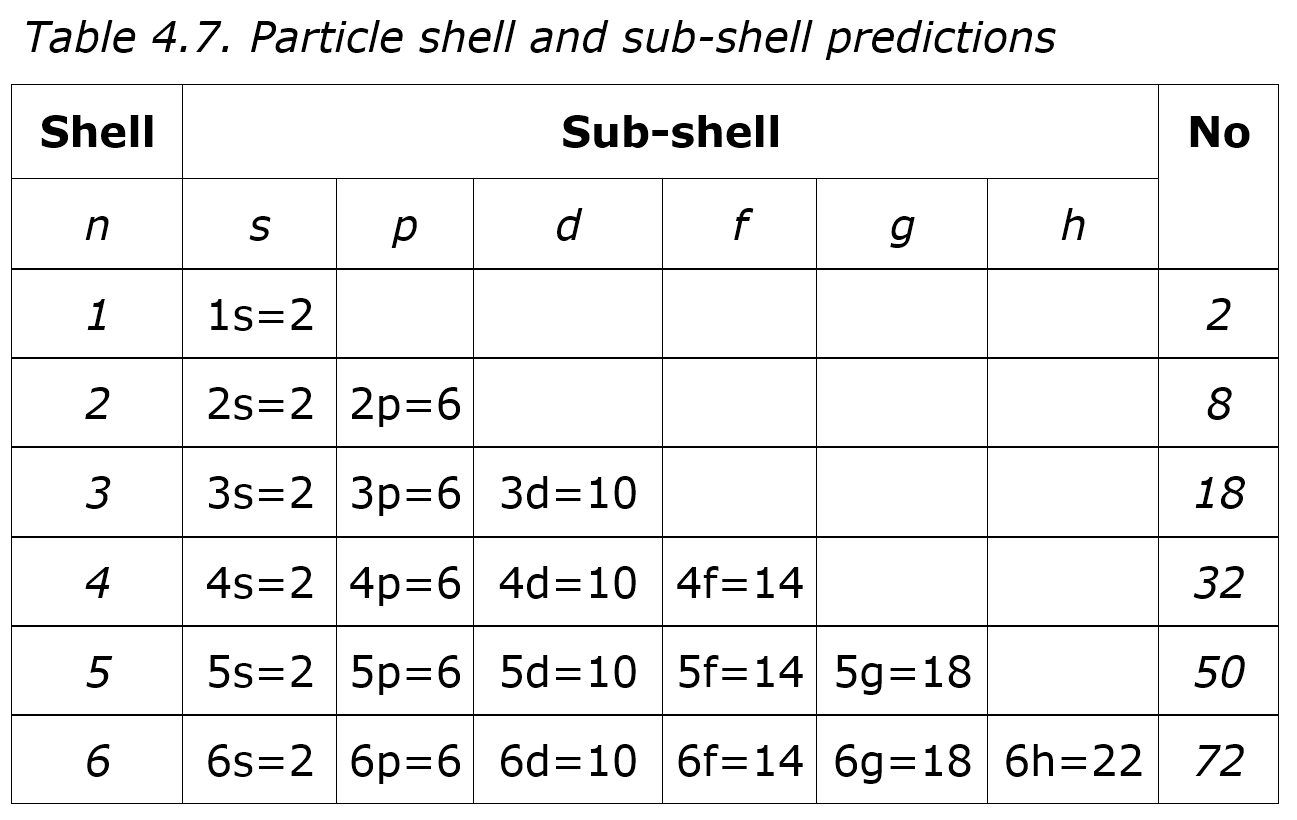
The problem was that the third row of the periodic table is still only eight elements, including the carbon and oxygen we need to live, and the expected eighteen elements only occur in the next row. The initial model predicted periodic table rows of 2, 8, 18, 32, 50, and 72 but instead the rows were 2, 8, 8, 18, 18, 32, and 32. So in the by now well-established practice, theory was fitted to fact by tweaking the model so the sub-shells fill in this odd order:
Row 1: 1s Hydrogen-Helium (two elements)
Row 2: 2s, 2p Lithium-Neon (eight elements)
Row 3: 3s, 3p Sodium-Argon (eight elements)
Row 4: 4s, 4p, 3d Potassium-Krypton (eighteen elements)
Row 5: 5s, 5p, 4d Rubidium-Xenon (eighteen elements)
Row 6: 6s, 6p, 5d, 4f Cesium-Radon (thirty-two elements)
Row 7: 7s, 7p, 6d, 5f Francium-? (thirty-two elements)
Note that the third sub-shell 3d is pushed down to row 4, so generations of chemistry students had to learn that Argon completes the third shell without one of its sub-shells. Obviously, this denies what a sub-shell is but if anyone asked why, the answer was because it does! And it does because the model was fitted to the facts.
Now instead of rules based on abstract numbers, let electrons be waves with the properties:
1. Shell. The circumference around the atom nucleus that allows the electron’s lowest wavelength.
2. Sub-shell. The harmonics that the shell circumference allows.
3. Direction. The wave direction, where waves at right angles don’t interfere.
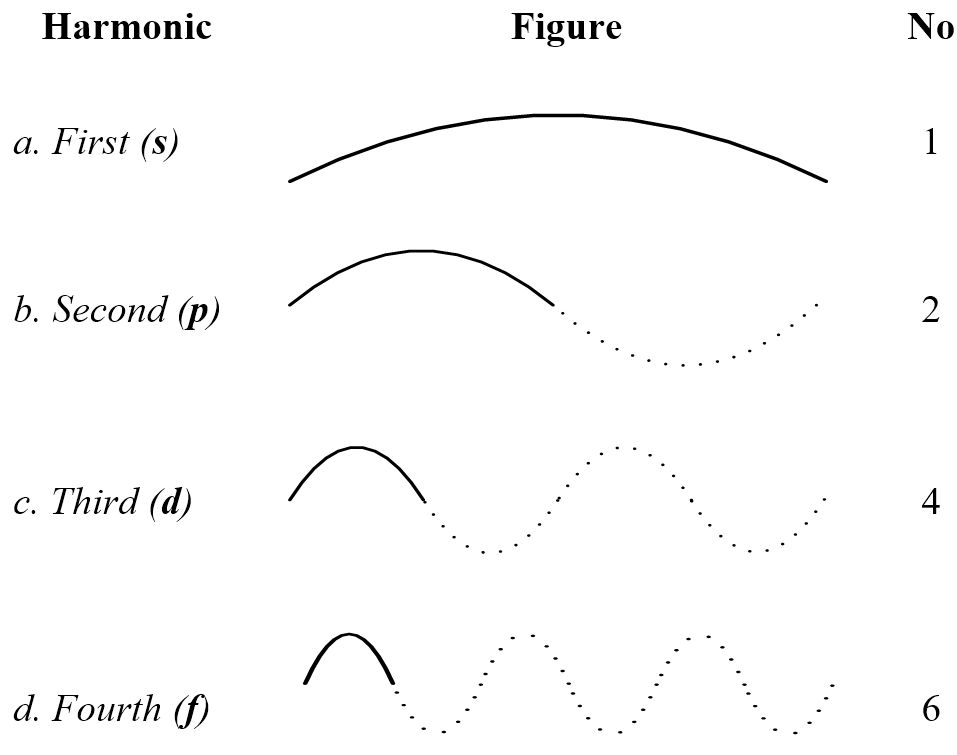
In music, a wave harmonic arises when a fundamental wave length lets other waves occur as well, so a fundamental and its harmonics can overlap at the same time. Figure 4.23 shows how a fundamental length can accommodate three additional harmonic levels, where the number at the right is how many harmonic waves occur for each level.
That sub-shells are wave harmonics then explains the rows of the periodic table as follows:
1. The first shell is the orbit circumference that lets a wave vibrate up and down on alternate cycles (Figure 4.23a). In this model, it is extreme light whose wavelength can’t be reduced, so there is only one harmonic, the 1s sub-shell. But a spherical orbit allows two directions at right angles, so it allows two waves at right angles that don’t interfere. The first shell then has one or two electron waves, so the first periodic table row is Hydrogen and the inert gas Helium.
2. The second shell orbit circumference is double that of the first, and allows two harmonics. The first is again a fundamental that alternates up and down, giving a 2s sub-shell that can hold two electrons. The second harmonic (Figure 4.23b) then allows two more waves at once, which for two directions is four electrons, and the complex harmonics of two-dimensional waves seen on a drum surface allow two more electrons, giving six in total for the 2p sub-shell. The second shell then allows eight electron waves, giving the second row of the periodic table, Lithium to Neon.
3. The third shell orbit circumference is triple that of the first, so it has a one and a half wave-length compared to the first. This again gives 3s and 3p sub-shells but the third harmonic can’t occur. A bipolar (up-down) wave can vibrate once on a string half its wavelength, and twice on a string of its wavelength, but a string one and a half times that gives nothing further. Adding a half-wavelength adds no new harmonics, so the third shell, like the second, only accommodates eight electrons, giving eight elements in the periodic table third row, so there is no 3d sub-shell.
4. The fourth shell is a two-wavelength circumference that quadruples the first. This allows a new harmonic that accommodates four waves, which for two directions is eight electrons (Figure 4.23c), plus two complex harmonics is ten. The 4s, 4p, and 4d sub-shells then give 18 elements in the periodic table fourth row, as observed.
5. The fifth shell, like the third, allows no new harmonic, so its 5s, 5p, and 5d sub-shells repeat the previous total of eighteen, giving the periodic table fifth row, again as observed.
6. The sixth shell allows a fourth f harmonic with six electrons (Figure 4.23d) which doubled is twelve, plus two complex harmonics is fourteen. This plus eighteen from the s, p, and d harmonics gives the thirty-two elements of the sixth periodic table row that include the Lanthanide series.
7. The seventh shell again has no new harmonic so it also has 32 elements, including the periodic table Actinide series.
An electron wave model based on sub-shell harmonics then fills the periodic table as follows:
1. 1s Hydrogen-Helium (2 elements)
2. 2s, 2p Lithium-Neon (8 elements)
3. 3s, 3p Sodium-Argon (8 elements)
4. 4s, 4p, 4d Potassium-Krypton (18 elements)
5. 5s, 5p, 5d Rubidium-Xenon (18 elements)
6. 6s, 6p, 6d, 6f Cesium-Radon (32 elements)
7. 7s, 7p, 7d, 7f Francium-? (32 elements)
Note that the third orbit has no 3d sub-shell and the fourth orbit has no 4f sub-shell, so electrons fill shells and their sub-shells in a logical order. Compare this to the strange order implied by quantum numbers (Figure 4.24), where by Klechkowski’s rule, the 3d sub-shell fills after the 4s sub-shell!
The properties of electrons in atoms are then not quantum numbers but:
1. Shell. The first shell circumference is the minimum wavelength of light and larger shells multiply this.
2. Sub-shell. Sub-shells are wave harmonics, where s is the first, p is the second, and so on.
3. Direction. The great circle axis orientation, where orthogonal waves don’t interfere.
Electrons then fill in the order observed in the periodic table, based on:
1. Shell. Each shell is a bigger orbit, which for an electron with mass means more processing and so more energy. Shells then fill in the order 1, 2, 3 … because smaller orbits need less energy.
2. Harmonic. Each sub-shell harmonic is a shorter wavelength for the same orbit, so again needs more energy. Sub-shells then fill in the order s, p, d … because lower harmonics need less energy.
Electron shells with sub-shells based on wave harmonics predict the periodic table without quantum numbers that need to be tweaked, so science can work forwards not backwards.