The last chapter described empty space as a three-dimensional surface that can vibrate, so light waves travel on the surface of space as water waves travel on the surface of a pool. This implies quantum directions ouside our space.
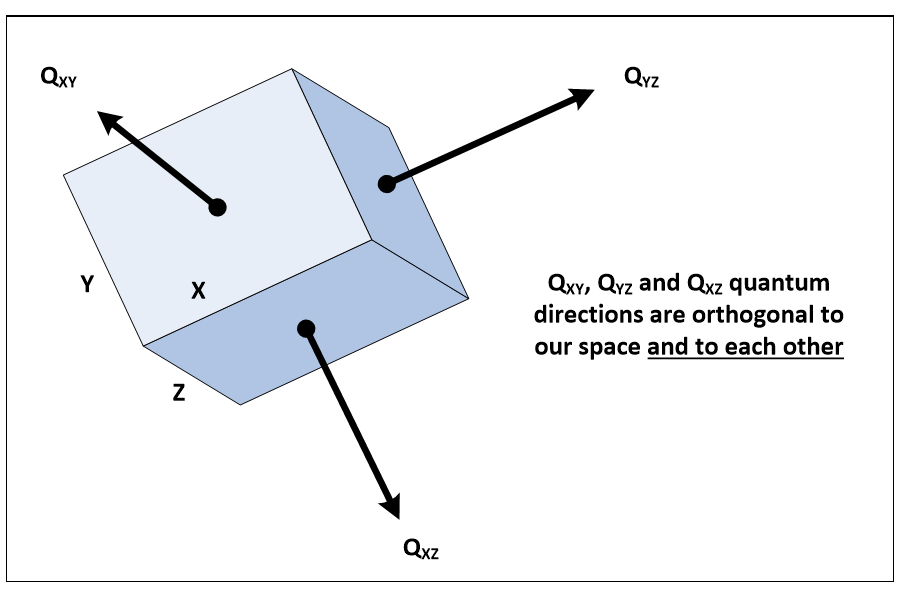
One might suppose that adding a dimension to a three-dimensional space adds one new direction but in mathematics, it adds three. In Figure 3.18, each of the three planes that cut through a point in our space has its own quantum direction outside space. Adding one dimension to our space then produces three new quantum directions, all at right angles to each other (Note 1).
Light is a transverse wave that vibrates at right angles to its polarization plane, in a direction that current physics calls imaginary. But if quantum directions exist, light passing through a point can vibrate in three directions, all at right angles to each other (Figure 3.18).
Light moving in a given direction however has only two independent ways to vibrate, as its movement uses up one dimension. Light can then polarize in two ways, vertical and horizontal, based on the two independent planes that cut its axis of movement. These polarizations are at right angles to each other, so a filter blocking vertical polarized light doesn’t block horizontal polarized light, and vice-versa.
Vertically polarized light vibrates in a quantum direction at right angles to horizontally polarized light, so what blocks one doesn’t block the other. They are independent vibrations but what happens when a polarization filter is turned on an angle?
Note 1: If physical space has dimensions (X, Y, Z), let quantum space have dimensions (X, Y, Z, Q), where Q is a fourth quantum dimension. A point in physical space with three orthogonal planes XY, XZ and YZ through it then has three orthogonal quantum directions outside our space. A photon with any polarization plane can vibrate into a quantum direction at right angles to it.