Processing explains electrons but what about their little brother, the neutrino? Our world needs electrons, as without them there is no chemistry, and so no life, but it also has vast numbers of a little nothing that until recently, we didn’t even know existed. The sun floods the earth with them every day but they mostly pass through it, like ghosts, so why did nature make so many of them?
The standard model expected neutrinos to have no mass at all, because they have no charge, but their tiny mass was how we detected them in the first place. When asked why neutrinos have no charge but a tiny mass, the current answer is that they just do, but we knew that already.
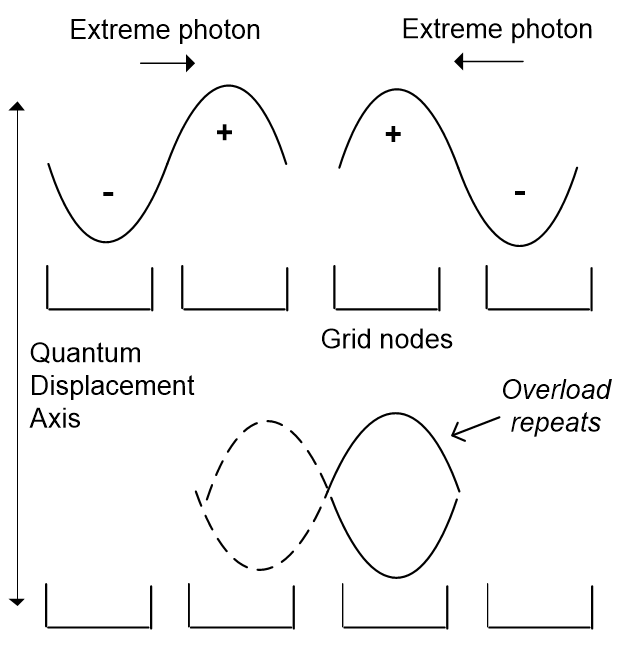
However processing allows another possibility, as if electrons arise when light collides in-phase, it can also collide out-of-phase. The result is that two points overload and one successfully reboots (Figure 4.3). Again, all the channels of an axis overload, but while heads meeting heads gives an electron bump, heads meeting tails gives the little nothing we call a neutrino. The neutrino is then the other option of an electron, not a useless building block.
Why then isn’t a neutrino’s mass exactly zero, as its charge is? If the quantum network was perfectly synchronous it would be, but that isn’t so (see 2.4.4). The photons in Figure 4.5 are slightly out of synch, so the heads and tails don’t exactly cancel but the remainder still does, giving a tiny mass but no charge.
For different neutrinos the asynchrony varies, so their mass also varies despite the zero charge. If an electron is a bump on space, a neutrino is a smudge, whose tiny mass comes from the asynchrony of the quantum network.
Table 4.2 below shows the processing that creates electrons and neutrinos with the properties of:
1. Stability. When the total processing fills the axis bandwidth, the entity produced is stable.
2. Mass. The net processing after opposite displacements cancel defines its mass.
3. Charge. The net remainder after opposite displacements cancel defines its charge.
Note that a tail-tail meet isn’t possible because it implies a prior head-head meet.
In summary, extreme light can overload one axis of a point of space to give a constant standing wave, which is an electron or neutrino, depending on phase. They are then brother leptons because both are one-dimensional matter, though to us, one is something and the other almost nothing.