It once seemed that light had energy but no mass, and matter had mass but no energy, until Einstein found that light had relativistic mass, and matter had a rest energy that a nuclear bomb could release. It then became apparent that mass and energy were somehow related.

Mass was originally defined as weight, that was later refined to be gravitational mass. Newton’s law that mass needed a force to accelerate it also led to the definition of inertial mass. They are different because a weightless object in space still needs a force to move it, so it has inertial mass but not gravitational mass. Momentum is mass times velocity, so a photon with no mass should have no momentum but solar sails move when the sun shines on them, and photons are bent by the sun’s gravity. This meant that a photon with no rest mass gains relativistic mass as it moves, so it has momentum (Note 1).

Light in contrast was originally seen as pure energy, which Planck’s equation related to its frequency. Einstein then did for matter what Planck had done for light, namely define its energy. In 1905, he deduced that the energy of matter is its mass times the speed of light squared, or as he put it: E=mc². This let us build atom bombs but it has never been clear why the energy of matter relates to light at all. If matter is an inert substance, why is its energy based on the speed of light?

If an electron is extreme photons repeatedly running in many channels, the energy of matter is the sum of their energy. Each channel contains a photon at the highest frequency whose energy is given by Planck’s equation. If these photons add to give the electron’s mass, which spreads in two dimensions not one, this predicts Einstein’s equation (Note 2). A processing model predicts E=mc², which Einstein proved based on how our physical world behaves. It follows that the energy of matter depends on the speed of light because matter is made of extreme light.

Next

Note 1. Relativistic mass is defined by special relativity. Rest mass is mass with no relativistic effects.

Note 2. Let the speed of light c=L_P/T_P, for Planck length L_P and Planck time T_P, and a photon’s energy E=h.f, by Planck’s equation. In this model, each electron channel essentially contains an extreme photon at a point with a frequency of 1/T_P, so its energy E=h/T_P. Now if Planck’s constant (h) is the transfer of one Planck process P over a Planck length in Planck time, h=P.L_P/T_P. Substituting gives E=P.L_P/T_P.T_P = E=P.c/T_P for the energy of one photon. Planck’s relation then also applies to an electron made of photons, except instead of h, the total processing is the electron’s mass m_e, which transfers over a unit sphere surface in time T_P, so the electron’s energy E= m_e.L_P.L_P/T_P.T_P, which is E= m_e.c². If all mass arises in the same way, then E= m.c² in general.

The standard model describes basic matter entities that have mass, charge, and energy, then accepts that mass equates to energy, based on Einstein’s equation, for no obvious reason except that it is so.

In contrast, a processing model equates mass and energy because matter is made of light. If matter is light repeating endlessly in a standing wave, then the energy of light and the mass of matter are just processing in different forms, and charge is also the net processing left-over. This model relates basic properties of physics that the standard model doesn’t connect in any way. Figure 4.16 summarizes these conclusions for mass, energy, and charge as follows:

1. Space. A point of empty space is null processing on a quantum network. The net process is zero, so it has no mass, the net process transfer averages zero, so it expresses no energy, and the process remainder is zero, so it has no charge.

2. Photon. A photon can’t stop to be weighed but at each point, it has a net process result, so it has mass, it transfers processing, so it has energy, and no process remainder means it has no charge.

3. Electron. An electron has a net process net result, so it has mass, it transfers processing as it moves, so it has energy, and its processing remainder gives it a negative charge.

4. Neutrino. A neutrino has a tiny process result, so it has a tiny mass, it transfers processing as it moves, so it has energy, but its processing remainders cancel, so it has no charge.

5. Quark. A quark has a net process result, so it has mass, it transfers processing as it moves, so it has energy, and its processing remainder gives one-third charges according to phase (up or down).

6. Anti-matter. Anti-matter versions of electrons, neutrinos, and quarks arise by reversing their processing. The result is the same mass but an opposite charge remainder.

In this model, space is a null process circle, light is space distributed, and matter is a standing wave of extreme light on one or more axes. Mass is the net process that repeats, charge is the net process left over, and energy is the rate of processing transfer. The basic properties of all the basic entities of physics then arise from processing.

Next

According to the standard model, neutrons decay when massive particles pop out of an invisible field to change them, but where did their mass come from? It had to come from somewhere, so the answer was, of course, another field! The standard model needed a Higgs field to provide mass for the virtual particles it had invented to explain its weak force. The whole model was at stake, so the search for a Higgs particle became the holy grail of physics. It attracted over 30 billion dollars in funding and finally in 2012, after a fifty-year search, CERN found a resonance in the right range to support its possible existence. Physicists all over the world breathed a sigh of relief, and some called it the God particle, perhaps because it answered their prayers. Finding a million, million, million, millionth of a second 125 GeV signal meant the standard model lived on! Yet the proposed Higgs particle:

1. Doesn’t explain mass. The Higgs particle doesn’t explain anything about the mass around us, nor does it add any value to general relativity, which is our best theory of mass to date, nor does it explain the dark energy and dark matter that is most of our universe. It only explains the mass of virtual particles that no-one has ever seen, in order to rescue the standard model:

“… the Higgs field allows us to reconcile … how … weak interactions work, that’s a far cry from explaining the origin of mass or why the different masses have the values they do.” (Wilczek,2008) p202

The Higgs isn’t about mass in general, just the mass invented by the standard model.

2. Is medieval logic. If the Higgs particle creates mass, what gives it mass? If another Higgs, what gives it mass, and so on? A Higgs particle that begets itself is indeed a God particle! Some say the field itself creates mass, but what then does the Higgs boson do? Weren’t bosons invented to avoid invisible fields causing visible effects in the first place? This logic, that like has to create like, was the medieval fallacy that what creates water has to be like water, but science debunked that by creating water from hydrogen and oxygen gases that aren’t watery at all. The idea that mass has to come from other mass is the same medieval logic that led nowhere in the past.

3. Is impossible by quantum theory. In a carefully crafted press release, CERN claimed that zero-spin would confirm the Higgs, then found it so, but quantum theory doesn’t allow a spin-zero point particle to have mass (Comay,2009). All quantum particles with mass have half spin, and only matter-antimatter mixes like mesons have zero spin. This suggests that the resonance CERN found came from a top or anti-top meson.

The Higgs is medieval logic, not based on quantum theory, that adds no value to our understanding of ordinary matter. That physics now calls it the origin of mass is a tribute to marketing not science. The irony is that a theory based on matter particles leads to the strange conclusion that mass is more virtual than physical:

“The Higgs mechanism is often said to account for the origins of mass in the visible universe. This statement, however, is incorrect. The mass of quarks accounts for only 2 percent of the mass of the proton and the neutron, respectively. The other 98 percent, we think, arises largely from the actions of gluons. But how gluons help to generate proton and neutron mass is not evident, because they themselves are massless.” (Et,Ulrich,& Venugopalan, 2015)

Nearly all the mass of an atom comes from its nucleus, but only 2% of the mass of protons and neutrons comes from their quark constituents, so virtual gluons are said to create the other 98%. The standard model therefore attributes most of the mass around us to massless virtual particles!

The Higgs is a virtual agent that was invented to explain another virtual agent that was invented to explain an observed effect, namely neutron decay. A model that uses one invisible thing to explain another becomes a theoretical house of cards, so it is no surprise that this so-called God particle hasn’t led to a single other discovery or benefit.

Next

A neutron is stable in a nucleus, but after about fifteen minutes in empty space, it turns into a proton. One of its down quarks flips, to become an up quark, turning the neutron into a proton. Again, the standard model needed some agent to cause this effect, and as gluons couldn’t do it, it proposed a new weak force that:

1. Affects all matter. Electromagnetism affects charge, and gluons affect quarks, but the weak force affects all matter.

2. Violates parity-symmetry. Weak interactions are left-right different.

3. Has no bound state. Electromagnetism binds atoms in molecules, the strong force binds nucleons in the nuclei, and gravity binds stars in galaxies, but the weak force binds nothing.

4. Is asymmetric. Neutrons decay into protons but protons are stable in space.

Neither electromagnetic nor strong forces act like this, so the standard model followed the by now standard practice of inventing a new field with new boson agents and charges. The new charge, called isospin (+½, –½), was retro-fitted to allow charm quarks to interact with down quarks but not up quarks, etc., as observed. But this time, the boson agents needed had to be heavier than protons, and a field that absorbed and emitted mass was unheard of.

Yet by now, virtual agents were the fashion and if the equations worked, it was accepted practice to prove they existed by finding matching accelerator resonances, so when in 1983 CERN found a million, million, million, millionth of a second event in the expected range, weak bosons immediately joined gluons in the standard model pantheon. On this flimsiest of evidence physicists today claim that:

“Experiments have observed three bosons that carry the weak force” (Marurger,2011), p221.

In fact, bosons haven’t been observed carrying anything. What was observed was just an accelerator event that is compatible with their existence. By analogy, suppose witness in a murder case said “I saw this knife killing the victim” and produced it as evidence, but cross-examination revealed that he just made a knife compatible with the wound and showed it in court. No jury in the land would accept that evidence, so why does physics call the same thing proof? CERN observed the energy spikes it created, not bosons carrying any force. No evidence at all links the CERN signal to neutron decay, so it proves nothing, yet physics now accepts that neutrons decay when a tiny 4.8 MEv down quark emits a massive 80,400 MEv W boson! This is like saying that an ant gave birth to an elephant.

It doesn’t help that the equations allow a neutron to decay in any of three ways (Figure 4.14), as it could:

1. Emit a W– that decays into an electron and anti-neutrino (Figure 4.14a)

2. Emit a W– boson that is hit by a neutrino to give an electron (Figure 4.14b)

3. Interact with a neutrino and a W+ boson to give an electron (Figure 4.14c).

Three different causes might seem better than one, but are three different alibis for a murder better than one? That a quark could emit a W- into a field, or could absorb a W+ from one, is the sort of after-the-fact reasoning that science is supposed to protect us from.

Even worse, the standard model equations are reversible, so protons should decay in empty space as neutrons do. This prediction led to a fruitless thirty-year search for proton decay, ending in the massive Kamioka experiment that estimated the free proton half-life to be over a billion, billion, billion years. The standard model predicts that protons will decay in space, but they don’t.

What then does a processing model predict? Recall that a neutron is one up and two down quarks, and a proton is two up and one down quark, so a neutron will change into a proton if one of its down quarks becomes an up quark.

Now add that a down quark is a photon head-head-tail collision, and an up quark is a photon head-tail-tail collision. Changing a down quark into an up quark then just requires a set of photon heads become tails.

Figure 4.15 shows that if a neutrino hits a photon head directly, it will turn into a tail and emit an electron. It follows that a neutrino hitting a neutron just right can turn it into a proton, as the beta decay equation describes (Note 1). However the reverse requires an electron to hit a quark, to turn its tails into heads, but getting an electron next to a quark takes a lot of energy, so proton decay only occurs in the heart of stars. This neutrino effect doesn’t alter the remainder so it isn’t electromagnetic, no photons are shared so it isn’t strong, and it affects any head-tail photon mix, which is all matter.

It follows that the weak effect, of neutron decay, can be attributed to neutrinos that are all around us. This predicts that neutrons won’t decay in a neutrino-free space, and that proton decay only occurs in stars, as it does. Again, the boson agents proposed by the standard model are entirely unnecesary.

Next

Note 1. In beta decay, a neutrino hitting a neutron can turn it into a proton by the equation N + ν → P⁺ + e⁻. Equally an electron can turn a proton into a neutron by inverse beta decay P⁺ + e⁻ → N + ν. Why insert fictional boson particles into these equations?

The atomic nucleus, once thought indivisible, is now known to consist of protons and neutrons that in turn are made up of quarks. A proton is two up quarks and a down quark, and a neutron is two down quarks and an up, so the odd quark charges add nicely to give a positive proton and a neutral neutron (Table 4.4). Could the quark structures proposed then combine to give stable protons and neutrons?

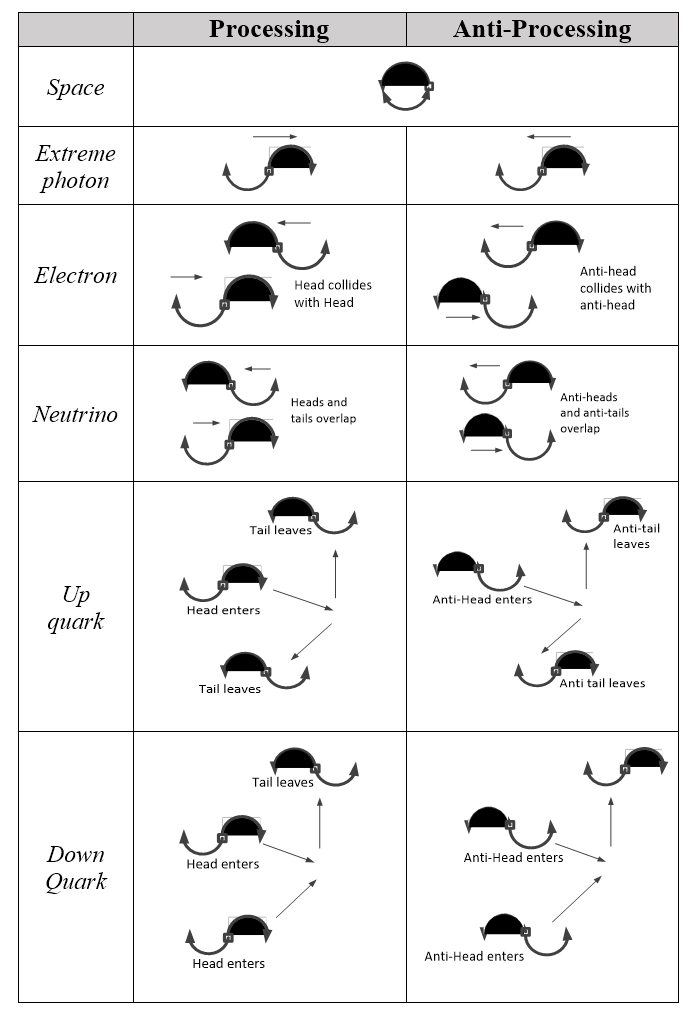
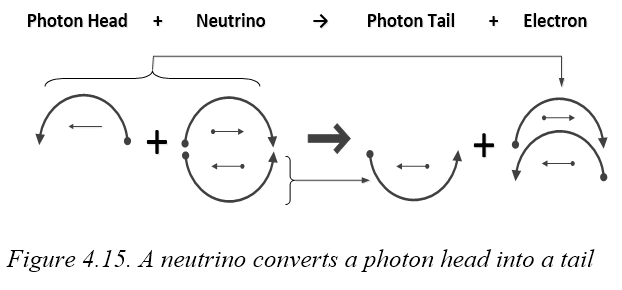
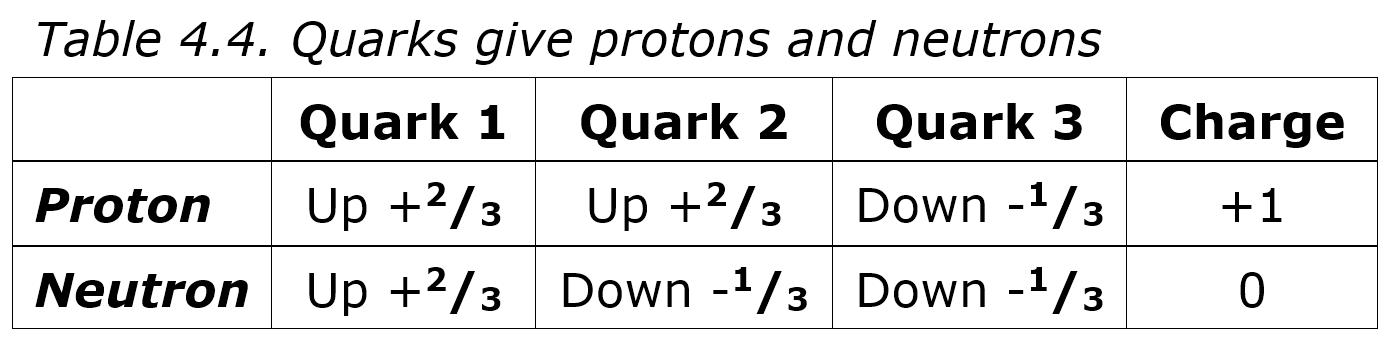
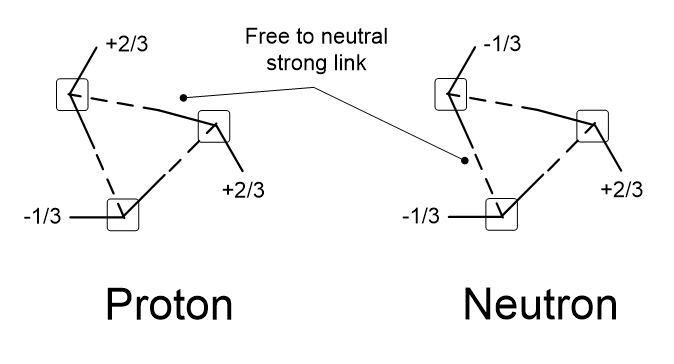
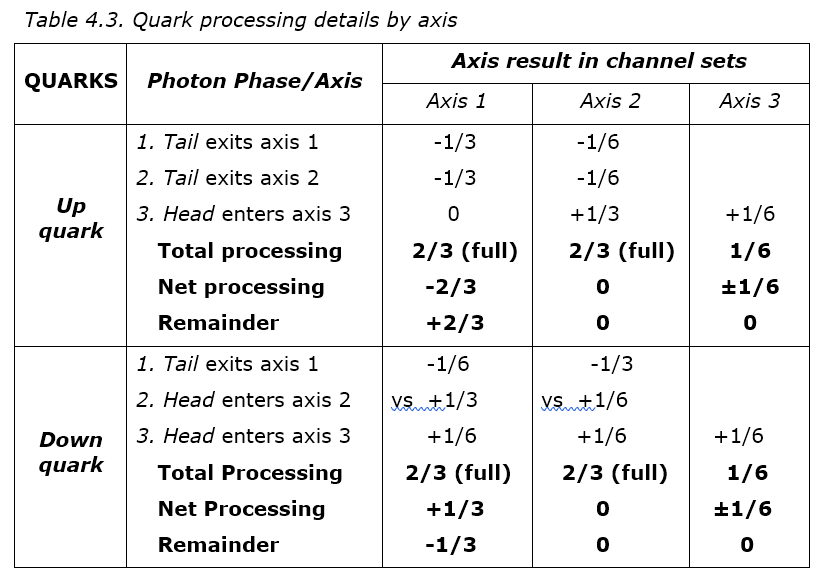
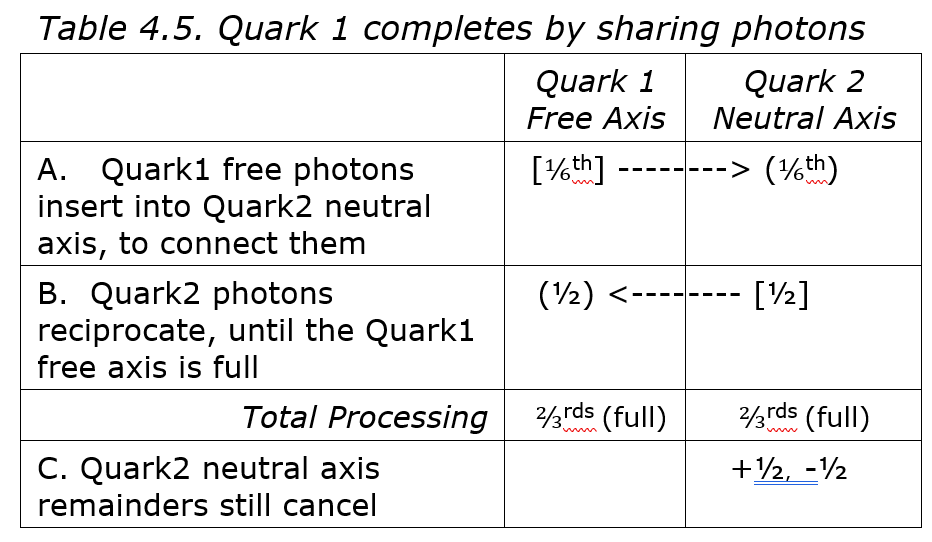Table 4.5 shows how two quarks could share photons to make one of them stable. In 4.5A, the free photons of one quark hook into the neutral axis of another, to give a sixth of an axis bandwidth in both quarks, with no remainder. In 4.5B, the photons from the second quark’s neutral axis return the favor until the first quark’s free axis is full, but because it shares an equal number of head and tail photons its remainders still cancel, and sharing doesn’t alter that it is full Both axes are now complete, and the neutral axis remainders still cancel (Table 4.5C). Photon sharing then stabilizes the first quark by filling its free axis.

This completes the first quark, but the second quark can also fill its free axis by linking to a third quark, that can fill its free axis by linking to the neutral axis of the first. In Figure 4.13, quarks in a triangle structure can share photons so they all become stable, and the result is a proton or neutron depending on the up or down quark mix. Now what binds the quarks isn’t magical gluons from nowhere but photon sharing, which pulls rather than pushes them together.

What then are the standard model’s red, blue, and green color charges? Each quark has to turn a different way to link in a triangle, so these charges are just its orientation. In the standard model world of inert particles, every change needs an agent to cause it but in a world of quantum events, every cycle explores a new option. event. Each photon tries to occupy any channel it can and if it fails, because another got there first, it just tries again. There is no predefined plan, just a free-for-all that tries every option, including different quark orientations.

To illustrate this, imagine pouring wine on a stack of empty glasses. When the water fills one glass, it just flows on to the next, until every glass is full. Nothing has to direct this activity, to decide which water ends up in which glass, as they always fill. Now suppose that when the water fills every glass, the weight restarts the system, so all the glasses empty and a new pouring cycle begins. Likewise, quarks explore every option to fill every channel, then a restart repeats the cycle.

In general, the quantum world tries every option until every channel overloads repeatedly, in a stable result that is a new entity. Protons, neutrons, electrons, and neutrinos then all form based on the same principle, which is the law of all action. Seeing matter as inert particles that only change when acted upon is like the nineteenth-century tabula rasa theory, that children are blank slates upon which we write. We no longer believe that, so why assume the whole universe is a blank slate? The quantum flux can push itself around, with no need for invisible particles from imaginary fields.

To recap, protons and neutrons form when quarks share photons in a triangle structure. The strong force that binds quarks together in the atomic nucleus is then based on photon sharing that occurs naturally when they orientate correctly, not gluons with color charges spawned by a strong field. But what then explains the weak field that the standard model also proposes?

Next

The forces that bind protons and neutrons in an atomic nucleus are so strong that when they break, the result is a nuclear explosion. Perhaps a bond that strong is necessary in order to overcome the huge electric repulsion between same charge protons. Hence, the standard model calls the force that holds quarks together in a nucleus the strong force. It has the odd property that it is zero at short range but increases as quarks separate, an effect analogous to stretching a rubber band. It exchanges no energy, so it isn’t electromagnetic, and increases with distance, so it isn’t gravity. The standard model needed a new force to explain how the atomic nucleus was held together.

Its answer was quantum chromodynamics, a field theory derived from quantum electrodynamics (QED), the theory that explains light. QED explains electromagnetism as perturbations caused when an electromagnetic field absorbs or emits photons, as shown in Feynman diagrams. Its calculations produced infinities, but they were removed by renormalization, a mathematical trick that arbitrarily subtracts infinities to get the finite answers desired.

Aiming to repeat the success of QED, quantum chromodynamics (QCD) proposed that a new strong field emitted particles called gluons that had a color charge. In essence, the strong field gluons acted to cause effects just as the electromagnetic field’s photons did. The gluons then used red, blue and green charges to bind quarks in a proton just as photons bind electrons in atoms, but with three values not two. The red, blue and green charges were said to cancel to white, just as positive and negative charges cancel to neutral. Three colors needed anti-colors to work, so to turn a red quark blue needs an anti-red gluon as well as a blue gluon. It was tricky, but the calculations worked, and in 1978 the PLUTO project managed to interpret a three-jet Upsilon event in gluon terms, so gluons joined the standard model particle pantheon. Meaning didn’t matter, so no-one asked why a universal field through all space existed for an effect that applied only to quarks.

A processing model approaches the same facts differently, based on reverse engineering rather than devising a field to fit the facts. The quark structure in Figure 4.11 shows it has free photons in one axis, so they could link quarks that are close together in a quark plasma. The free photons of one quark could insert themselves into another as shown in Figure 4.12, where an extreme photon has its head in one node and tail in another. It is now proposed that when quarks are side-by-side, the extra photons in a quark’s free axis insert themselves into a nearby quark like hooks.

This photon sharing would then give a bond that is initially zero but increases with distance, because as linked quarks separate, the shared photon wavelength increases to release the energy needed to pull them back together. The more the quarks separate, the stronger the effect, so quarks side-by-side experience no force but are pulled together as they separate. In effect, shared photons could be the elastic bands that hold quarks together. If the strong force is based on quarks sharing photons, could this let quarks combine to fill all the channels of a point plane to achieve stability?

Next

As for the lepton collision, a three-way collision has phase options that can be expressed in photon head-tail terms. Again, a tail-tail-tail meet isn’t possible as it implies a prior head-head-head event. The phase options are:

1. Head-head-head. Three sets of photon heads meeting at equal angles in a point will allocate processing equally, so each axis is only partly filled. There are free channels that let other entities in, so the result isn’t stable.

2. Head-tail-tail. In this case, two photon rays leave the point as another arrives, as shown in Figure 4.10a, and this is proposed to be an up quark.

3. Head-head-tail. In this case, one ray is leaving the point as the other two arrive, as shown in Figure 4.10b, and this is proposed to be a down quark.

Figure 4.10 shows the proposed up and down quark structures. Photons compete for channels on a first-come-first-served basis, so a three-way meeting raises the issue of interaction order. If a photon head entering a node meets a photon tail leaving it, the tail must have started before the head, or it would be a head, giving the rule that tails fill channels first. Using this rule, Table 4.3 gives the expected axis bandwidth result as before, but now there are three axes not one, and each fills at two-thirds not one. Again, the total processing defines axis stability, the mass is the net processing, and the charge is the net remainder.

The details are:

1. Up quark. If two extreme photon rays leave the point as another arrives, the tails first fill axis 1, giving a plus two-thirds charge remainder on what can be called its charge axis. The remaining tail photons then combine with later arriving heads to fill a neutral axis, as the remainders cancel. The remaining head photons then partly to fill the third free axis to a sixth of its two-thirds maximum. The result has a two-thirds charge, and is stable on two axes, but the third axis isn’t filled.

2. Down quark. If one ray is leaving a node as the other two arrive, the tail photons first cancel opposing heads to fill a neutral axis, as the remainders cancel. Then the heads and the remaining tails fill a charge axis, with a minus third charge left over. This again leaves a third free axis partly filled to a sixth instead of two thirds. The result has a minus third charge, and is again stable on two axes, but again the third axis isn’t filled.

This result is interesting because it gives the correct third charges for quarks, which no other model does. The standard model allocates one-third charges to quarks after the fact, but this model derives them from photons. It predicts that quarks occupy one node like leptons but only fill two of the three collision axes.

To sum up, the three-axis structure derived for quarks is:

1. Charge axis. Fills with charge of +⅔ for an up quark, and -⅓ for a down quark.

2. Neutral axis. Fills with no charge as heads and tails cancel with no remainder.

3. Free axis. Remaining one sixth of head photons partly fills this axis.

Figure 4.11 summarizes the proposed quark axis structure. Note that the axes are at 60° even though the photons meet at 120° because quarks are head-tail mixes, and so some rays are leaving as others arrive.

The quark structure proposed isn’t stable, but this fits the fact that quarks never exist alone. And their symmetric structure may allow a group of them maintain an exterior of stable axes. Yet quarks are stable in a nucleus, so they must somehow link to fill all the channels of a plane, or the model fails. Physics calls the link between quarks the strong force.

Next

Lambert’s cosine law is that the intensity of a light ray hitting a surface varies by the cosine of the angle it hits at, so light hitting at right angles to a plane gives all its intensity, but light parallel to plane gives none. In angle degree terms, light at right angles is 90º which has a cosine of one, and parallel light is 0º which has a cosine of zero, so the formula works. It also works for an in-between angle, where the cosine of that angle gives the intensity. Essentially, light projects its intensity onto a plane according to angle.

A processing model explains this rule in channel terms. A ray of light can occupy all the channels of a point on its axis, so it has full intensity on that axis. But on other axis channels, its strength projects according to their angle, so the cosine law applies. Rays of light on the same axis then share the same channels because Cos(0) is one, and rays at right angles share no channels because Cos(90) is zero. In-between, the rays share channels based on the cosine of the angle between them. In effect, the cosine law also explains how photons fill the channels of a point.

The last section explained electrons and neutrinos as extreme light colliding on a line through a point. This section explores whether a three-way collision of extreme light in a plane through a point can do the same for quarks. Can the same logic applied to a line for electrons be extended to a plane for quarks? For an electron, the photons had to fill the bandwidth of a line, which was taken to be one. Two light rays crossing at a point occupy entirely different channels, so it makes sense that the bandwidth of a plane through a point is two. It follows that if two extreme light rays are needed to fill the channels of a line through a point, four extreme light rays are needed to fill a plane though it.

In Figure 4.9, three equal-angle extreme rays in a plane meet at a point, so they aren’t enough to fill the bandwidth of a plane. Each ray fills half the bandwidth of one axis, but three times that is 1.5 not two, so the result can’t be stable because there are unfilled channels that another entity could exploit.

However the result could be semi-stable if some axes are filled completely. Dividing the plane bandwidth of two between three axes gives each one a two-thirds bandwidth, so could this interaction fill any of these axes? Three extreme light rays could fill the channels of two of the axes but leave the third unfilled.

Next

In the standard model, quarks are fundamental point particles, unrelated to electrons or neutrinos. They come in two types, called up and down, with different charges. An up quark has a plus two-thirds charge, and a down quark has a minus one-third charge. This lets two up quarks and a down quark combine into a positively charged proton that form the nucleus of Hydrogen, the first element of the periodic table. Each new periodic table element has one more proton plus some neutrons that arise from one up quark and two down quarks. Quarks form the protons and neutrons in the nuclei of all known atoms.

If an electron’s mass comes from a one-axis collision of extreme photons, quark mass must also arise in same way. The last section covered all the ways photons can collide on one axis, so a quark can’t be a one-axis result, but it could be a three-way interaction. If three rays of extreme light meet at a point, they must be on the same plane, as shown in Figure 4.9. Again, such an event is unlikely but again, it must have occurred in the early plasma by the quantum law of all action.

A three-axis collision has an interesting symmetry, as photons on any axis half exist on the other two by the cosine rule, so any quark axis is one ray vs. two others at half strength, which is a lepton type collision. But applying this feature to one axis doesn’t leave enough light to do the same to the other two.

It follows that this extreme light interaction isn’t stable alone, but physics tells us that unlike electrons, quarks are so unstable that they never exist alone. Had it not been so this model would fail, as few other reverse engineering options exist, but could quark processing fill all the channels of a plane through a point, just as electrons did for a line through a point?

Next

All the matter we see is made of atoms, whose mass comes almost entirely from their nuclei, which are made of quarks. Quarks, not electrons, represent what we call matter, but particle physics struggles to explain them. For example, their charges come in unexpected thirds for no known reason. Yet they obey the equations of matter, so a model that explains electrons must also explain quarks.

QR4.4.1 A Three-way Interaction

QR4.4.2 Filling a Plane

QR4.4.3 Quark Phases

QR4.4.4 The Strong Force

QR4.4.5 Protons and Neutrons

QR4.4.6 The Weak Force

QR4.4.7 The God Particle

QR4.4.8 Mass and Energy

QR4.4.9 Review

Next