Quantum spin is so strange that when Pauli first proposed it, he wasn’t believed:

“… the spin of a fundamental particle has the curious feature that its magnitude always has the same value, although the direction of its spin axis can vary…” (Penrose, 1994), p270.

A physical particle spins in a rotation plane around an axis of rotation (Figure 3.17), so its axis must be known to measure its spin. Measuring spin on an axis that isn’t its rotation axis gives less than the total spin. If the spin axis is unknown, one must measure spin on three orthogonal axes to get the total spin. In contrast, the spin of a quantum entity measured on any axis is always the same, so quantum spin doesn’t work like physical spin.

In this model, detecting a photon’s spin on any axis gives all its spin for the same reason that detecting it always gives all its energy. In both cases, a physical event, is an all or nothing restart of the photon, including all its energy or spin, so this property is expected.

Physics measures quantum spin in units of Planck’s constant in radians (Note 1). If Planck’s constant represents the linear transfer of one Planck process, as proposed earlier, Planck’s constant in radians will then represent its units of angular transfer, or spin, so this is also expected.

Finally, according to quantum theory, quantum spin occurs in both directions at once, so measuring it gives either spin direction randomly. Just as a photon can go through two slits at the same time but is randomly in one or the other, so it also spins both ways and is randomly either. Essentially, the quantum law of all action applies to rotational as well as linear movement. A photon can rotate in two directions at once just as it goes through two slits at once. The measured spin result is then random because it depends on server access, so this property of quantum spin is also expected.

Spin is then a fundamental property of every quantum entity because processing spreads in angular as well as linear directions, and its properties are as expected.

Note 1. Quantum spin is defined as Plank’s reduced constant ħ = h/2p (in angular radians).

Next

In physics, quantum spin is a mathematical construct applied to quantum particles. Like quantum waves, it is said to be imaginary so when electrons spin, nothing is assumed to actually spin, because if an electron is a particle with no size, how can it spin? And if it had a size, its edges would have to move faster than light to explain the observed effects. Physics calls quantum spin imaginary because it is physically impossible, but what if it isn’t? If the process behind a quantum wave is a transverse circle, there is no reason why it can’t actually spin. 

QR3.7.1. The Curious Case of Quantum Spin

QR3.7.2. Quantum Directions

QR3.7.3. Polarization

Next

Super-computers running a million-million cycles a second take millions of seconds (months) to emulate not just what a photon does in a million-millionth of a second, but what it does in a million-millionth of that (Wilczek, 2008), (p113). Why do these tiniest bits of the universe, with no known internal structure, need so much computing to emulate? The answer proposed is that a photon isn’t a tiny particle taking a single path but a processing wave spreading over many paths.

How then do photons travel? Feynman’s sum over histories method predicts how light goes from A to B by calculating all possible paths, then choosing the one with the least action integral (Feynman et al., 1977) p26-7. It is based on quantum theory, so it predicts perfectly, but like its source, became a method that works not a theory that happens, because it describes what can’t physically happen.

But if a photon is a processing wave, then Feynman’s method works because its instances really do take all possible paths, and the first to trigger a physical event is where we see it arrive. A photon doesn’t need to know the fastest path in advance if it takes every path, as the instance that happens to arrive first reincarnates it in a physical event. This makes its path the one the photon took, and the restart removes all the other instances, like a magician removing the evidence of how a trick is done after it happens.

The physical law of least action that has puzzled science for centuries is then explained by a quantum of all action. A particle can’t know the fastest path to an unknown destination in advance, but the photon just takes every path and lets the first physical result decide its path.

To recap, knowing nothing in advance, the photon spreads down every path, and restarts when it reaches a detector, as only a processing wave can. What reaches a detector by the fastest route isn’t a solitary particle that magically knows the best path in advance, but a quantum ensemble that explores every path and disbands when the job is done.

Every physical event then arises from a myriad of quantum events. The quantum world tries every option and the physical world takes the best and ignores the rest, so if this isn’t the best of all possible worlds as Leibniz said, it isn’t for lack of trying. The world we live in isn’t the only possible world but of all possibilities, it could be the best it can be. Just as a photon tries every path before picking the best, if our universe did the same, it couldn’t be any better.

The physical law of least action then derives from the quantum law of all action that:

Everything that can happen as a physical event, does happen as a quantum event.

This is equivalent to Feynman’s everything that can happen does happen (Cox & Forshaw, 2011), as well as Gellman’s quantum totalitarian principle that everything not forbidden is compulsory. Both imply that quantum events explore every possibility before a physical event occurs. The law of all action is universal, so it applies not only to how light travels but also to quantum spin.

Next

In 1662 Fermat amended Hero’s law to be the path of least time because when light enters water, where it travels slower, it refracts to take the fastest path not the shortest path. In Figure 3.15, light takes the path that bends as it enters water, not the dotted shortest path, because it is faster.

To understand this, suppose the photon is a lifeguard trying to save a drowning swimmer as quickly as possible. The fastest path to the swimmer isn’t the dotted straight line but the solid bent line because the lifeguard can run faster than he swims, so it is better to run further down the beach, then swim a shorter distance. The dotted line is the shortest path but the solid line is the fastest, and that is the path light takes in Figure 3.15. But while a lifeguard might know in advance that path is fastest, how does refracting light know this?

In 1752, Maupertuis generalized further that:

“The quantity of action necessary to cause any change in Nature always is the smallest possible”.

Euler, Leibnitz, Lagrange, Hamilton, and others then developed the mathematics of the law of least action, that nature always does the least work, sparking a furious theological debate on whether we live in the best of all possible worlds. Despite Voltaire’s ridicule, how light always finds the path of least action, for any destination, remained a mystery.

For example, light bouncing off the mirror in Figure 3.16 could take any of the dotted paths shown, but according to optics, always takes the solid line fastest path. But as a photon moves forward in time to trace out its path, how does it at each stage know the fastest route? As Feynman says:

“Does it ‘smell’ the neighboring paths to find out if they have more action?” (Feynman et al., 1977), p19-9.

To say that a photon chooses in advance the path of least action is to get causality backwards. That a photon, the simplest of all things, with no known internal mechanism, always finds the fastest path to any destination, for any media combination, any path complexity, any number of alternate paths, and inclusive of relativity, is simply miraculous. The law of least action is a physical law that is no better understood today than it was centuries ago, but like all physical laws, it has its basis in a quantum law.

Next

He was correct that if light moves as a wave, it should bend round corners as sound waves do, but actually it does. In 1660 Grimaldi found that light does bend but less than sound because its wavelength is shorter. The question is then, how can a spreading wave travel in a straight line?

Detecting photons by screens at different distances confirms this, as the results aren’t a perfect straight line but randomly spread about (Figure 3.14). A physical particle would have to travel in a zigzag path to explain this! When a photon moves, it is most likely to exist in a straight line, but the wave itself spreads in all directions.

Next

That light always finds the best path to any destination has puzzled thinkers for centuries. Hero of Alexandria observed that light always takes the shortest path but how does it know what that is? It might seem obvious that it is a straight line but how, at each step, does light know what straight is? (Note 1) How light always finds the best path to any destination is still a mystery today.

QR3.6.1. A Wave Moves

QR3.6.2. The Law of Least Action

QR3.6.3. The Law of All Action

Note 1. By relativity, light doesn’t always travel in a straight line, so “straightness” is not self-evident.

Next

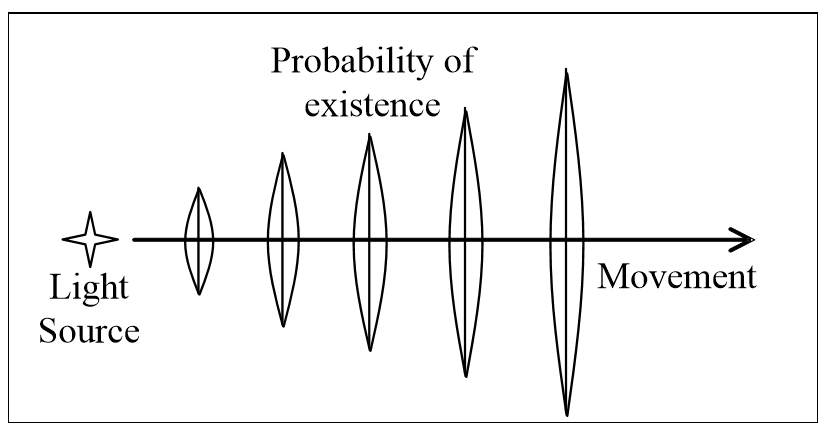
What then decides where a photon hits a screen? The photon wave spreads to many screen points, but only hits one point. That point is random, like a lottery where everyone has a chance, but quantum theory says the hit chance is higher where the wave is stronger. More precisely, the photon’s probability to hit at each point depends on the square of its net amplitude there. These probabilities add up to one, so it always hits somewhere, but exactly where doesn’t depend on any physical history. Quantum theory then explains two-slit interference as follows:

1. The photon wave spreads through both slits.

2. It then interferes with itself to give a net amplitude at many screen points.

3. This amplitude squared is the photon’s probability to hit each point.

4. Where it actually hits is then randomly chosen from these probabilities.

5. The result is the interference pattern seen.

After the photon wave spreads through both slits, its positive or negative amplitudes combine at the screen to give a net strength whose square predicts its probability to hit there. Then a random value between zero and one decides where the photon actually hits, regardless of its physical history.

This predicts the interference pattern seen, but how can imaginary waves do this? If quantum waves are imaginary, are physicists like shamans who see the future in a dream? Real physics requires real quantum waves, and they can be if they are processing waves. When this wave overloads a screen, many points will reboot, to request a server restart, and the server response will be either:

1. Access. The server accepts the request to restart at that point, so it no longer supports the rest of the wave, which collapses. This then is a physical event at that point, OR,

2. No access. The server doesn’t respond that cycle because it is busy elsewhere, so the point just carries on. This then was a potential physical event that didn’t happen.

Quantum collapse is then a winner takes all lottery run by the server. When many instances overload many screen points, the reboot request that accesses the server wins the prize of being the photon, leaving the rest of the wave to wither on the grid. And just as in our lotteries, more tickets mean more chance of success, so points that access the server more frequently are more likely to restart it.

Quantum theory says that a photon’s probability to hit depends on its wave amplitude squared at each point. Light is a sine wave, so its amplitude squared is its power, which for a processing wave means more server access. If positive and negative amplitudes cancel at the server, the net power at each point decides the number of instructions needed, and hence server access. It follows that points where the wave has more power will access the server more, and so be more likely to restart it. The probabilities to hit of quantum theory are then based on the net amplitude squared because for a processing wave, that decides the server access that restarts it in a physical event. The strange logic of quantum theory then makes sense for a processing wave.

To recap, photon instances overload many screen points, but which one actually restarts the wave is to us unknown, i.e. random. Even so, the net wave power at each point defines access to the server, so it predicts the probability to restart there. The two-slit experiment can now be described as follows:

a. Photon wave instances spread through both slits.

b. Those that reach the same screen point by different paths interfere.

c. The first instance to restart the wave server is where the photon hits.

d. The wave power at each point predicts that because it decides server access.

The mysteries of Young’s experiment (3.1.3) are now resolved. How can a photon go through two slits but still arrive at one screen point? A particle can’t do this, but a processing wave spreading on a network can restart at a point. How can sending one photon at a time through two slits still produce an interference pattern? Again, a particle can’t go through two slits or interfere with itself, but a processing wave can. Why then does light come in little photon packets, as Einstein showed? Physical waves don’t come in packets, but processing needs a fundamental process, and that is a photon. Why doesn’t the photon wave smear over a screen as a wave would? A physical wave doesn’t hit at a point, but one process with one server restarts at one point as an all-or-nothing event.

A detector put in one of the two slits only fires half the time, but it isn’t because half the photons go through each slit. Every photon always goes through both slits, but each detector only wins the quantum lottery half the time, as the server is attending to other slit instances the rest of the time. Likewise, detectors in both slits fire equally often, but it isn’t because photon particles choose between the slits equally. Again, each photon always takes both slits but it can only restart in one, as decided by a server that attends equally to all its instances. This mechanism now answers questions like:

a. Does one photon go through both slits at once? Yes, photon instances go through both slits.

b. Does it hit the screen at one point? Yes, the whole photon process restarts at one screen point.

c. Did it take a particular path? Yes, the instance that restarted the photon took a specific path.

d. Did it also take all other possible paths? Yes, other instances, now disbanded, took every path.

Table 3.1 below compares Feynman’s summary of quantum mechanics (Feynman et al., 1977), p37-10 with a processing wave approach. Both approaches predict the same results, but the first is a recipe with no rationale, while the second is based on processing reasons. What made no sense fifty years ago now makes sense based on network processing.  

We now consider another mystery of light that has baffled scientists for centuries.

Next

Table 3.1. Quantum mechanics in processing wave terms
Quantum Mechanics	Processing Wave
1. Existence. The probability a quantum entity exists is the absolute square of its complex quantum amplitude value at a point in space	1. Existence. The probability that a processing wave restarts in a physical event depends on server access that varies as the square of its amplitude at a point in space
2. Interference. If a quantum event can occur in two alternate ways, the positive and negative amplitudes combine, i.e. they interfere	2. Interference. If a processing wave reaches a point by alternate paths, the positive and negative amplitudes combine, i.e. they interfere
3. Observation. Observing one path lets the other occur without interference, so the outcome probability is the simple sum of the alternatives, i.e. the interference is lost	3. Observation. Observing a processing wave on one path lets the other occur without interference, so the outcome probability is the simple sum of the alternatives, i.e. the interference is lost

 

If a photon is a spread-out wave, as quantum theory says, how can it arrive at a point? A wave should hit a barrier as a smear, but a photon hits a screen as a dot instead. Radio waves are many meters long, so they should take time to arrive, even at light speed, but they don’t. If they did, in the delay between a wave front’s first hit and the rest arriving, the tail could hit something else. One photon could hit twice, but it never does! Physical waves deliver their energy over time and space, but a quantum wave delivers all its energy instantly at a point, which is strange. As Walker says:

“How can electromagnetic energy spread out like a wave … still be deposited all in one neat package when the light is absorbed?” (Walker, 2000), p43.

Current physics can’t explain how any wave could collapse instantly to a point:

“After more than seven decades, no one understands how or even whether the collapse of a probability wave really happens.” (Greene, 2004), p119.

Einstein rejected quantum collapse because it implied faster than light travel, for as he argued:

Before the photon hits a screen, its wave function exists at points A or B with some probability but after, it is entirely at point A say not at B. The moment A knows it is the photon, then B knows it isn’t. Now suppose the screen is moved further away, eventually A and B could be in different galaxies, so how can the collapse happen instantly? That two events anywhere in the universe are instantly correlated faster than light contradicts special relativity.

Physical waves don’t collapse instantly but a processing wave can suddenly restart. In our computing, a processing device restart is called a reboot. When a phone, laptop, or printer reboots, it restarts its processing from scratch. A network point is the same but if it is a client, it will request a processing restart from its server. A reboot has the following properties:

1. It is irreversible. A reboot can’t be undone because the restart loses all prior processing.

2. It conserves processing. The amount of processing before and after a reboot is the same.

3. It re-allocates processing. A reboot will allocate the processing involved in new ways.

For example, if you are doing things on your phone and turn it off and on again, it reboots. When it restarts, it re-allocates its processing to show new things, so what you were doing before is probably lost irretrievably. A reboot essentially just restarts a processing device from scratch.

Sometimes a phone or computer will reboot itself. The usual trigger for this is that it overloads, which means it was doing something and ran out of processing. A network client that overloads will do the same, except it will request a processing restart from the server that supports it.

If quantum processing is the same, a network point that overloads will also reboot and request a server restart. Now consider a photon wave arriving at a screen. The points of the screen are already fully occupied generating its matter, so when the photon’s processing arrives, they will overload and request a server restart. The photon is a wave, so many points will reboot at once, all requesting a server restart, but one photon has only one server, so only one request can succeed. The photon will then restart at the point that successfully restarts the photon server, which is where it hits the screen.

In computing terms then, quantum collapse is a processing wave restart caused by a reboot. Many instances arrive at many screen points, but only one of them can restart the photon. When this happens, the instances with no server support just disappear instantly, as quantum theory says. Quantum collapse is then the inevitable disbanding of child instances when their parent server begins a new child. The wave collapses instantly, as if it never was, because instances have no substance.

Why then doesn’t the reboot point overload again when its processing restarts? The pass-it-on protocol (2.4.4) avoids this, because the point passes on its processing before doing anything else, so the photon that caused the overload just starts to spread again.

To recap, a photon arriving at a screen isn’t a lonely particle heading for a single hit point but a wave of many instances, any of which can restart the photon. When a screen blocks this wave, where it restarts depends on which reboot request the server accepts, which to us is random. Many points may request a restart, but only one can succeed, and the first to do so is where the photon hits the screen.

Why then does quantum collapse occur faster even than light? The speed of light depends on how fast the screen of our space refreshes, but a program can change a pixel without any screen movement. It can just change it directly, anywhere on the screen. Likewise, a photon server can directly change its clients anywhere on the screen of our space. The point-to-point screen speed that defines the speed of light is thus irrelevant to the server-client effect of quantum collapse. Quantum collapse can occur faster than light because it is a server effect, not a client effect.

Materialism sees quantum collapse as things disappearing but in computing terms, it is just client events that didn’t happen. When electrons collide and bounce apart, materialism sees the same particles entering and leaving, but quantum theory tells another story, that the electrons leaving the collision are actually brand-new creations, fresh off the quantum press. A world of things can just sit there and exist, but a world of processing events must be constantly recreated. It follows that the entities physics observes, like photons and electrons, are constantly annihilated and recreated rather than permanently existing.

Next

Einstein, like Newton, assumed that light particles follow a fixed path from source to screen, so where it hits should be predictable, but it isn’t exactly so. Photons shot in the same way at a screen don’t all hit at the same point. Quantum theory explains this by saying that each photon hits the screen at a random point, chosen from the possibilities. Einstein concluded that there were two options: either quantum theory was wrong or there were hidden physical causes:

“This is the fundamental problem: either quantum mechanics is incomplete and needs to be completed by a theory of hidden quantities, or it is complete and then the collapse of the wave function must be made physically plausible. This dilemma has not been solved until today, but on the contrary has become more and more critical.” (Audretsch, 2004), p73.

This problem, which Einstein raised and Bohr ignored, still haunts physics today. All attempts to find physical variables that explain quantum randomness have failed, as have all attempts to show that quantum theory is incomplete. The problem then is that quantum theory works perfectly but it allows random events that have no physical explanation to this day.

What then is the resolution? Both theories, that quantum theory is incomplete or that it is physical, have led nowhere, so the answer must lie elsewhere. Materialism assumes that quantum theory is either incomplete or physical, but if it is wrong, quantum theory could be true and not physical. We know that quantum theory always works, and we know that it can’t be physical, so perhaps both are true. We then can’t find hidden variables to explain randomness because there are none, and we can’t find a fault in quantum theory because there is none. If quantum events create physical events, as quantum theory says, then randomness could arise from outside the physical domain. 

For example, the laws of Minecraft don’t explain how its blocks exist, nor do the laws of chess say how its pieces exist, because that is outside their domain. A created scenario can never completely explain itself, so perhaps physical laws can’t explain randomness for the same reason. If I turn off a game, or tip over a chess board, it is an event outside the game domain. Likewise, randomness in our world could come from quantum events that occur outside the physical domain, but what could they be?

Next

According to quantum theory, quantum waves spread until they collapse in a physical event, but how can a wave that can be bigger than a galaxy instantly collapse to a point? And why is that that point random, not based on any physical history?

QR3.5.1. Hidden Variables?

QR3.5.2. Quantum Collapse

QR3.5.3. The Quantum Lottery

Next